
科目: 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).在以坐标原点为极点,
为参数).在以坐标原点为极点,![]() 轴正半轴为极轴的极坐标系中,曲线
轴正半轴为极轴的极坐标系中,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)写出![]() 的普通方程和
的普通方程和![]() 的直角坐标方程;
的直角坐标方程;
(2)若![]() 与
与![]() 相交于
相交于![]()
![]() 两点,求
两点,求![]() 的面积.
的面积.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆![]() 的左顶点为
的左顶点为![]() ,右焦点为
,右焦点为![]() ,点
,点![]() 在椭圆
在椭圆![]() 上.
上.
(1)求椭圆![]() 的方程;
的方程;
(2)若直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,直线
两点,直线![]() 分别与
分别与![]() 轴交于点
轴交于点![]() ,在
,在![]() 轴上,是否存在点
轴上,是否存在点![]() ,使得无论非零实数
,使得无论非零实数![]() 怎样变化,总有
怎样变化,总有![]() 为直角?若存在,求出点
为直角?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】某品牌汽车4S店,对该品牌旗下的A型、B型、C型汽车进行维修保养,汽车4S店记录了100辆该品牌三种类型汽车的维修情况,整理得下表:
车型 | A型 | B型 | C型 |
频数 | 20 | 40 | 40 |
假设该店采用分层抽样的方法从上述维修的100辆该品牌三种类型汽车中随机取10辆进行问卷回访.
(1)求A型、B型、C型各车型汽车抽取的数目;
(2)维修结束后这100辆汽车的司机采用“100分制”打分的方式表示对4S店的满意度,按照大于等于80为优秀,小于80为合格,得到如下列联表:
优秀 | 合格 | 合计 | |
男司机 | 10 | 38 | 48 |
女司机 | 25 | 27 | 52 |
合计 | 35 | 65 | 100 |
问能否在犯错误概率不超过0.01的前提下认为司机对4S店满意度与性别有关系?请说明原因.
(参考公式: )
)
附表:
| 0.100 | 0.050 | 0.010 | 0.001 |
K | 2.706 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目: 来源: 题型:
【题目】关于圆周率![]() ,数学发展史上出现过许多有创意的求法,如著名的普丰实验和查理斯实验.受其启发,我们也可以通过设计下面的实验来估计
,数学发展史上出现过许多有创意的求法,如著名的普丰实验和查理斯实验.受其启发,我们也可以通过设计下面的实验来估计![]() 的值:先请120名同学每人随机写下一个x,y都小于1的正实数对
的值:先请120名同学每人随机写下一个x,y都小于1的正实数对![]() ,再统计其中x,y能与1构成钝角三角形三边的数对
,再统计其中x,y能与1构成钝角三角形三边的数对![]() 的个数m,最后根据统计个数m估计
的个数m,最后根据统计个数m估计![]() 的值.如果统计结果是
的值.如果统计结果是![]() ,那么可以估计
,那么可以估计![]() 的值为( )
的值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数![]() ,其中
,其中![]() 为实数,
为实数,![]() 为自然对数的底数.
为自然对数的底数.
(1)求函数![]() 的单调区间;
的单调区间;
(2)是否存在实数![]() ,使得对任意给定的
,使得对任意给定的![]() ,在区间
,在区间![]() 上总存在三个不同的
上总存在三个不同的![]() ,使得
,使得![]() 成立?若存在,求出实数
成立?若存在,求出实数![]() 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】2019年电商“双十一”大战即将开始.某电商为了尽快占领市场,抢占今年“双十一”的先机,对成都地区年龄在15到75岁的人群“是否网上购物”的情况进行了调查,随机抽取了100人,其年龄频率分布表和使用网上购物的人数如下所示:(年龄单位:岁)
年龄段 |
|
|
|
|
|
|
频率 | 0.1 | 0.32 | 0.28 | 0.22 | 0.05 | 0.03 |
购物人数 | 8 | 28 | 24 | 12 | 2 | 1 |
(1)若以45岁为分界点,根据以上统计数据填写下面的![]() 列联表,并判断能否在犯错误的概率不超过0.001的前提下认为“网上购物”与年龄有关?
列联表,并判断能否在犯错误的概率不超过0.001的前提下认为“网上购物”与年龄有关?
年龄低于45岁 | 年龄不低于45岁 | 总计 | |
使用网上购物 | |||
不使用网上购物 | |||
总计 |
(2)若从年龄在![]() ,
,![]() 的样本中各随机选取2人进行座谈,记选中的4人中“使用网上购物”的人数为
的样本中各随机选取2人进行座谈,记选中的4人中“使用网上购物”的人数为![]() ,求随机变量
,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
参考数据:
| 0.025 | 0.010 | 0.005 | 0.001 |
| 3.841 | 6.635 | 7.879 | 10.828 |
参考公式: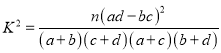
查看答案和解析>>
科目: 来源: 题型:
【题目】如图①,是由矩形![]() ,
,![]() 和
和![]() 组成的一个平面图形,其中
组成的一个平面图形,其中![]() ,
,![]() ,将其沿
,将其沿![]() 折起使得
折起使得![]() 重合,连接
重合,连接![]() 如图②.
如图②.
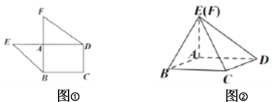
(1)证明:平面![]() 平面
平面![]() ;
;
(2)若![]() 为线段
为线段![]() 中点,求直线
中点,求直线![]() 与平面
与平面![]() 所成角的正切值.
所成角的正切值.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数![]() 有极值,且导函数
有极值,且导函数![]() 的极值点是
的极值点是![]() 的零点,给出命题:①
的零点,给出命题:①![]() ;②若
;②若![]() ,则存在
,则存在![]() ,使得
,使得![]() ;③
;③![]() 与
与![]() 所有极值之和一定小于0;④若
所有极值之和一定小于0;④若![]() ,且
,且![]() 是曲线
是曲线![]() 的一条切线,则
的一条切线,则![]() 的取值范围是
的取值范围是![]() .则以上命题正确序号是_____________.
.则以上命题正确序号是_____________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com