
科目: 来源: 题型:
【题目】某农科站技术员为了解某品种树苗的生长情况,在该批树苗中随机抽取一个容量为100的样本,测量树苗高度(单位:cm).经统计,高度均在区间[20,50]内,将其按[20,25),[25,30),[30,35),[35,40),[40,45),[45,50]分成6组,制成如图所示的频率分布直方图,其中高度不低于40cm的树苗为优质树苗.
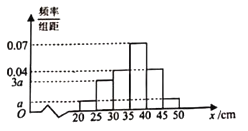
(1)已知所抽取的这100棵树苗来自于甲、乙两个地区,部分数据如下2×2列联表所示,将列联表补充完整,并根据列联表判断是否有99.9%的把握认为优质树苗与地区有关?
(2)用样本估计总体的方式,从这批树苗中随机抽取4棵,期中优质树苗的棵数记为X,求X的分布列和数学期望.
甲地区 | 乙地区 | 合计 | |
优质树苗 | 5 | ||
非优质树苗 | 25 | ||
合计 |
附:K2=![]() ,其中n=a+b+c+d
,其中n=a+b+c+d
P(K2≥k0) | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目: 来源: 题型:
【题目】已知双曲线C:![]() =1(a>0,b>0)的左右焦点为F1,F2过点F1的直线l与双曲线C的左支交于AB两点,△BF1F2的面积是△AF1F2面积的三倍,∠F1AF2=90°,则双曲线C的离心率为( )
=1(a>0,b>0)的左右焦点为F1,F2过点F1的直线l与双曲线C的左支交于AB两点,△BF1F2的面积是△AF1F2面积的三倍,∠F1AF2=90°,则双曲线C的离心率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】 已知函数f(x)=|x+a|+|x-2|.
(1)当a=-3时,求不等式f(x)≥3的解集;
(2)若f(x)≤|x-4|的解集包含[1,2],求a的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】(选修4-4 坐标系与参数方程) 以平面直角坐标系的原点为极点, ![]() 轴的正半轴为极轴建立极坐标系,设曲线C的参数方程为
轴的正半轴为极轴建立极坐标系,设曲线C的参数方程为 (
(![]() 是参数),直线
是参数),直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的直角坐标方程和曲线C的普通方程;
的直角坐标方程和曲线C的普通方程;
(2)设点P为曲线C上任意一点,求点P到直线![]() 的距离的最大值.
的距离的最大值.
查看答案和解析>>
科目: 来源: 题型:
【题目】某房产销售公司从登记购房的客户中随机选取了50名客户进行调查,按他们购一套房的价格(万元)分成6组:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 得到频率分布直方图如图所示.用频率估计概率.
得到频率分布直方图如图所示.用频率估计概率.
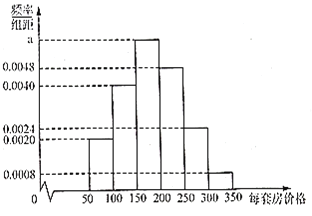
房产销售公司每卖出一套房,房地产商给销售公司的佣金如下表(单位:万元):
房价区间 |
|
|
|
|
|
|
佣金收入 | 1 | 2 | 3 | 4 | 5 | 6 |
(1)求![]() 的值;
的值;
(2)求房产销售公司卖出一套房的平均佣金;
(3)若该销售公司平均每天销售4套房,请估计公司月(按30天计)利润(利润=总佣金-销售成本).
该房产销售公司每月(按30天计)的销售成本占总佣金的百分比按下表分段累计/span>计算:
月总佣金 | 不超过100万元的部分 | 超过100万元至200万元的部分 | 超过200万元至300万元的部分 | 超过300万元的部分 |
销售成本占 佣金比例 |
|
|
|
|
查看答案和解析>>
科目: 来源: 题型:
【题目】在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)若![]() ,求曲线
,求曲线![]() 与
与![]() 的交点坐标;
的交点坐标;
(2)过曲线![]() 上任一点
上任一点![]() 作与
作与![]() 夹角为30°的直线,交
夹角为30°的直线,交![]() 于点
于点![]() ,且
,且![]() 的最大值为
的最大值为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】由国家统计局提供的数据可知,2012年至2018年中国居民人均可支配收入![]() (单位:万元)的数据如下表:
(单位:万元)的数据如下表:
年份 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 |
年份代号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
人均可支配收入 | 1.65 | 1.83 | 2.01 | 2.19 | 2.38 | 2.59 | 2.82 |
(1)求![]() 关于
关于![]() 的线性回归方程(系数精确到0.01);
的线性回归方程(系数精确到0.01);
(2)利用(1)中的回归方程,分析2012年至2018年中国居民人均可支配收入的变化情况,并预测2019年中国居民人均可支配收入.
附注:参考数据:![]() ,
,![]() .
.
参考公式:回归直线方程![]() 的斜率和截距的最小二乘估计公式分别为:
的斜率和截距的最小二乘估计公式分别为: 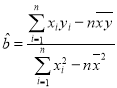 ,
,![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】《九章算术》中《方田》章有弧田面积计算问题,计算术曰:以弦乘矢,矢又自乘,并之,二而一.其大意是,弧田面积计算公式为:弧田面积![]() (弦乘矢+矢乘矢),弧田是由圆弧(简称为弧田的弧)和以圆弧的端点为端点的线段(简称 (弧田的弦)围成的平面图形,公式中“弦”指的是弧田的弦长,“矢”等于弧田的弧所在圆的半径与圆心到弧田的弦的距离之差.现有一弧田,其弦长
(弦乘矢+矢乘矢),弧田是由圆弧(简称为弧田的弧)和以圆弧的端点为端点的线段(简称 (弧田的弦)围成的平面图形,公式中“弦”指的是弧田的弦长,“矢”等于弧田的弧所在圆的半径与圆心到弧田的弦的距离之差.现有一弧田,其弦长![]() 等于
等于![]() ,其弧所在圆为圆
,其弧所在圆为圆![]() ,若用上述弧田面积计算公式计算得该弧田的面积为
,若用上述弧田面积计算公式计算得该弧田的面积为![]() ,则
,则![]() ( )
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)若![]() ,求曲线
,求曲线![]() 与
与![]() 的交点坐标;
的交点坐标;
(2)过曲线![]() 上任一点
上任一点![]() 作与
作与![]() 夹角为30°的直线,交
夹角为30°的直线,交![]() 于点
于点![]() ,且
,且![]() 的最大值为
的最大值为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com