
科目: 来源: 题型:
【题目】某企业拥有3条相同的生产线,每条生产线每月至多出现一次故障.各条生产线是否出现故障相互独立,且出现故障的概率为![]() .
.
(1)求该企业每月有且只有1条生产线出现故障的概率;
(2)为提高生产效益,该企业决定招聘名维修工人及时对出现故障的生产线进行维修.已知每名维修工人每月只有及时维修1条生产线的能力,且每月固定工资为1万元.此外,统计表明,每月在不出故障的情况下,每条生产线创造12万元的利润;如果出现故障能及时维修,每条生产线创造8万元的利润;如果出现故障不能及时维修,该生产线将不创造利润,以该企业每月实际获利的期望值为决策依据,在![]() 与
与![]() 之中选其一,应选用哪个?(实际获利=生产线创造利润-维修工人工资)
之中选其一,应选用哪个?(实际获利=生产线创造利润-维修工人工资)
查看答案和解析>>
科目: 来源: 题型:
【题目】某游戏棋盘上标有第![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 站,棋子开始位于第
站,棋子开始位于第![]() 站,选手抛掷均匀硬币进行游戏,若掷出正面,棋子向前跳出一站;若掷出反面,棋子向前跳出两站,直到跳到第
站,选手抛掷均匀硬币进行游戏,若掷出正面,棋子向前跳出一站;若掷出反面,棋子向前跳出两站,直到跳到第![]() 站或第
站或第![]() 站时,游戏结束.设游戏过程中棋子出现在第
站时,游戏结束.设游戏过程中棋子出现在第![]() 站的概率为
站的概率为![]() .
.
(1)当游戏开始时,若抛掷均匀硬币![]() 次后,求棋子所走站数之和
次后,求棋子所走站数之和![]() 的分布列与数学期望;
的分布列与数学期望;
(2)证明:![]() ;
;
(3)若最终棋子落在第![]() 站,则记选手落败,若最终棋子落在第
站,则记选手落败,若最终棋子落在第![]() 站,则记选手获胜.请分析这个游戏是否公平.
站,则记选手获胜.请分析这个游戏是否公平.
查看答案和解析>>
科目: 来源: 题型:
【题目】目前,中国有三分之二的城市面临“垃圾围城”的窘境. 我国的垃圾处理多采用填埋的方式,占用上万亩土地,并且严重污染环境. 垃圾分类把不易降解的物质分出来,减轻了土地的严重侵蚀,减少了土地流失. 2020年5月1日起,北京市将实行生活垃圾分类,分类标准为厨余垃圾、可回收物、有害垃圾和其它垃圾四类 .生活垃圾中有30%~40%可以回收利用,分出可回收垃圾既环保,又节约资源. 如:回收利用1吨废纸可再造出0.8吨好纸,可以挽救17棵大树,少用纯碱240千克,降低造纸的污染排放75%,节省造纸能源消耗40%~50%.
现调查了北京市5个小区12月份的生活垃圾投放情况,其中可回收物中废纸和塑料品的投放量如下表:
|
|
|
|
| |
废纸投放量(吨) | 5 | 5.1 | 5.2 | 4.8 | 4.9 |
塑料品投放量(吨) | 3.5 | 3.6 | 3.7 | 3.4 | 3.3 |
(Ⅰ)从![]() 这5个小区中任取1个小区,求该小区12月份的可回收物中,废纸投放量超过5吨且塑料品投放量超过3.5吨的概率;
这5个小区中任取1个小区,求该小区12月份的可回收物中,废纸投放量超过5吨且塑料品投放量超过3.5吨的概率;
(Ⅱ)从![]() 这5个小区中任取2个小区,记
这5个小区中任取2个小区,记![]() 为12月份投放的废纸可再造好纸超过4吨的小区个数,求
为12月份投放的废纸可再造好纸超过4吨的小区个数,求![]() 的分布列及期望.
的分布列及期望.
查看答案和解析>>
科目: 来源: 题型:
【题目】为了解贵州省某州2020届高三理科生的化学成绩的情况,该州教育局组织高三理科生进行了摸底考试,现从参加考试的学生中随机抽取了100名理科生,,将他们的化学成绩(满分为100分)分为![]()
![]()
![]()
![]()
![]()
![]() 6组,得到如图所示的频率分布直方图.
6组,得到如图所示的频率分布直方图.
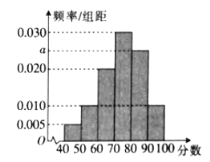
(1)求a的值;
(2)记A表示事件“从参加考试的所有理科生中随机抽取一名学生,该学生的化学成绩不低于70分”,试估计事件A发生的概率;
(3)在抽取的100名理科生中,采用分层抽样的方法从成绩在![]() 内的学生中抽取10名,再从这10名学生中随机抽取4名,记这4名理科生成绩在
内的学生中抽取10名,再从这10名学生中随机抽取4名,记这4名理科生成绩在![]() 内的人数为X,求X的分布列与数学期望.
内的人数为X,求X的分布列与数学期望.
查看答案和解析>>
科目: 来源: 题型:
【题目】黄冈“一票通”景区旅游年卡,是由黄冈市旅游局策划,黄冈市大别山旅游公司推出的一项惠民工程,持有旅游年卡一年内可不限次畅游全市19家签约景区.为了解市民每年旅游消费支出情况![]() 单位:百元
单位:百元![]() ,相关部门对已游览某签约景区的游客进行随机问卷调查,并把得到的数据列成如表所示的频数分布表:
,相关部门对已游览某签约景区的游客进行随机问卷调查,并把得到的数据列成如表所示的频数分布表:
组别 |
|
|
|
|
|
频数 | 10 | 390 | 400 | 188 | 12 |
![]() 求所得样本的中位数
求所得样本的中位数![]() 精确到百元
精确到百元![]() ;
;
![]() 根据样本数据,可近似地认为市民的旅游费用支出服从正态分布
根据样本数据,可近似地认为市民的旅游费用支出服从正态分布![]() ,若该市总人口为750万人,试估计有多少市民每年旅游费用支出在7500元以上;
,若该市总人口为750万人,试估计有多少市民每年旅游费用支出在7500元以上;
![]() 若年旅游消费支出在
若年旅游消费支出在![]() 百元
百元![]() 以上的游客一年内会继续来该景点游玩现从游客中随机抽取3人,一年内继续来该景点游玩记2分,不来该景点游玩记1分,将上述调查所得的频率视为概率,且游客之间的选择意愿相互独立,记总得分为随机变量X,求X的分布列与数学期望.
以上的游客一年内会继续来该景点游玩现从游客中随机抽取3人,一年内继续来该景点游玩记2分,不来该景点游玩记1分,将上述调查所得的频率视为概率,且游客之间的选择意愿相互独立,记总得分为随机变量X,求X的分布列与数学期望.
![]() 参考数据:
参考数据:![]() ,
,![]() ;
;![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】人们常说的“幸福感指数”就是指某个人主观地评价他对自己目前生活状态的满意程度的指标,常用区间![]() 内的一个数来表示,该数越接近
内的一个数来表示,该数越接近![]() 表示满意度越高.为了解某地区居民的幸福感情况,随机对该地区的男、女居民各
表示满意度越高.为了解某地区居民的幸福感情况,随机对该地区的男、女居民各![]() 人进行了调查,调查数据如表所示:
人进行了调查,调查数据如表所示:
幸福感指数 |
|
|
|
|
|
男居民人数 |
|
|
|
|
|
女居民人数 |
|
|
|
|
|
(1)估算该地区居民幸福感指数的平均值;
(2)若居民幸福感指数不小于![]() ,则认为其幸福.为了进一步了解居民的幸福满意度,调查组又在该地区随机抽取
,则认为其幸福.为了进一步了解居民的幸福满意度,调查组又在该地区随机抽取![]() 对夫妻进行调查,用
对夫妻进行调查,用![]() 表示他们之中幸福夫妻(夫妻二人都感到幸福)的对数,求
表示他们之中幸福夫妻(夫妻二人都感到幸福)的对数,求![]() 的期望(以样本的频率作为总体的概率).
的期望(以样本的频率作为总体的概率).
查看答案和解析>>
科目: 来源: 题型:
【题目】某服装加工厂为了提高市场竞争力,对其中一台生产设备提出了甲、乙两个改进方案:甲方案是引进一台新的生产设备,需一次性投资1000万元,年生产能力为30万件;乙方案是将原来的设备进行升级改造,需一次性投入700万元,年生产能力为20万件.根据市场调查与预测,该产品的年销售量的频率分布直方图如图所示,无论是引进新生产设备还是改造原有的生产设备,设备的使用年限均为6年,该产品的销售利润为15元/件(不含一次性设备改进投资费用).
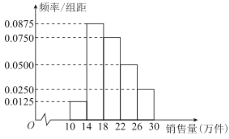
(1)根据年销售量的频率分布直方图,估算年销量的平均数![]() (同一组中的数据用该组区间的中点值作代表);
(同一组中的数据用该组区间的中点值作代表);
(2)将年销售量落入各组的频率视为概率,各组的年销售量用该组区间的中点值作年销量的估计值,并假设每年的销售量相互独立.
①根据频率分布直方图估计年销售利润不低于270万元的概率:
②若以该生产设备6年的净利润的期望值作为决策的依据,试判断该服装厂应选择哪个方案.(6年的净利润=6年销售利润-设备改进投资费用)
查看答案和解析>>
科目: 来源: 题型:
【题目】高三年级某班50名学生期中考试数学成绩的频率分布直方图如图所示,成绩分组区间为:![]()
![]()
![]()
![]()
![]()
![]()
![]() .其中a,b,c成等差数列且
.其中a,b,c成等差数列且![]() .物理成绩统计如表.(说明:数学满分150分,物理满分100分)
.物理成绩统计如表.(说明:数学满分150分,物理满分100分)
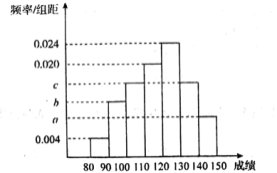
分组 |
|
|
|
|
|
频数 | 6 | 9 | 20 | 10 | 5 |
(1)根据频率分布直方图,请估计数学成绩的平均分;
(2)根据物理成绩统计表,请估计物理成绩的中位数;
(3)若数学成绩不低于140分的为“优”,物理成绩不低于90分的为“优”,已知本班中至少有一个“优”同学总数为6人,从此6人中随机抽取3人,记X为抽到两个“优”的学生人数,求X的分布列和期望值.
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系中![]() ,以原点
,以原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴,建立极坐标系,直线
轴正半轴为极轴,建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() ,曲线
,曲线![]() 的参数方程为:
的参数方程为: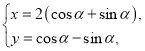 (
(![]() 为参数),
为参数),![]() ,
,![]() 为直线
为直线![]() 上距离为
上距离为![]() 的两动点,点
的两动点,点![]() 为曲线
为曲线![]() 上的动点且不在直线
上的动点且不在直线![]() 上.
上.
(1)求曲线![]() 的普通方程及直线
的普通方程及直线![]() 的直角坐标方程.
的直角坐标方程.
(2)求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)写出曲线![]() 的极坐标方程,并求出曲线
的极坐标方程,并求出曲线![]() 与
与![]() 公共弦所在直线的极坐标方程;
公共弦所在直线的极坐标方程;
(2)若射线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,与曲线
两点,与曲线![]() 交于
交于![]() 点,且
点,且![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com