
科目: 来源: 题型:
【题目】定义在![]() 上的函数
上的函数![]() 同时满足以下条件:①
同时满足以下条件:①![]() 在
在![]() 上为减函数,
上为减函数,![]() 上是增函数;②
上是增函数;②![]() 是偶函数;③
是偶函数;③![]() 在
在![]() 处的切线与直线
处的切线与直线![]() 垂直.
垂直.
(1)求函数![]() 的解析式;
的解析式;
(2)设![]() ,若对
,若对![]()
![]() ,使
,使![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为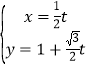 (
(![]() 为参数),在以坐标原点为极点,
为参数),在以坐标原点为极点,![]() 轴的正半轴为极轴的极坐标系中,曲线
轴的正半轴为极轴的极坐标系中,曲线![]() 的极坐标方程为
的极坐标方程为![]() (
(![]() 且
且![]() ).
).
(I)求直线![]() 的极坐标方程及曲线
的极坐标方程及曲线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)已知![]() 是直线
是直线![]() 上的一点,
上的一点,![]() 是曲线
是曲线![]() 上的一点,
上的一点, ![]() ,
,![]() ,若
,若![]() 的最大值为2,求
的最大值为2,求![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】据长期统计分析,某货物每天的需求量![]() 在17与26之间,日需求量
在17与26之间,日需求量![]() (件)的频率
(件)的频率![]() 分布如下表所示:
分布如下表所示:
需求量 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 |
频率 | 0.12 | 0.18 | 0.23 | 0.13 | 0.10 | 0.08 | 0.05 | 0.04 | 0.04 | 0.03 |
已知其成本为每件5元,售价为每件10元.若供大于求,则每件需降价处理,处理价每件2元.假设每天的进货量必需固定.
(1)设每天的进货量为![]() ,视日需求量
,视日需求量![]() 的频率为概率
的频率为概率![]() ,求在每天进货量为
,求在每天进货量为![]() 的条件下,日销售量
的条件下,日销售量![]() 的期望值
的期望值![]() (用
(用![]() 表示);
表示);
(2)在(1)的条件下,写出![]() 和
和![]() 的关系式,并判断
的关系式,并判断![]() 为何值时,日利润的均值最大?
为何值时,日利润的均值最大?
查看答案和解析>>
科目: 来源: 题型:
【题目】设一个正三棱柱![]() ,每条棱长都相等,一只蚂蚁从上底面
,每条棱长都相等,一只蚂蚁从上底面![]() 的某顶点出发,每次只沿着棱爬行并爬到另一个顶点,算一次爬行,若它选择三个方向爬行的概率相等,若蚂蚁爬行10次,仍然在上底面的概率为
的某顶点出发,每次只沿着棱爬行并爬到另一个顶点,算一次爬行,若它选择三个方向爬行的概率相等,若蚂蚁爬行10次,仍然在上底面的概率为![]() ,则
,则![]() 为( )
为( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】法国有个名人叫做布莱尔·帕斯卡,他认识两个赌徒,这两个赌徒向他提出一个问题,他们说,他们下赌金之后,约定谁先赢满5局,谁就获得全部赌金700法郎,赌了半天,甲赢了4局,乙赢了3局,时间很晚了,他们都不想再赌下去了.假设每局两赌徒输赢的概率各占![]() ,每局输赢相互独立,那么这700法郎如何分配比较合理( )
,每局输赢相互独立,那么这700法郎如何分配比较合理( )
A.甲400法郎,乙300法郎B.甲500法郎,乙200法郎
C.甲525法郎,乙175法郎D.甲350法郎,乙350法郎
查看答案和解析>>
科目: 来源: 题型:
【题目】已知直线![]() 过椭圆
过椭圆![]() 的右焦点
的右焦点![]() ,抛物线
,抛物线![]() 的焦点为椭圆
的焦点为椭圆![]() 的上顶点,且
的上顶点,且![]() 交椭圆
交椭圆![]() 于
于![]() 两点,点
两点,点![]() 在直线
在直线![]() 上的射影依次为
上的射影依次为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)若直线![]() 交
交![]() 轴于点
轴于点![]() ,且
,且![]() ,当
,当![]() 变化时,证明:
变化时,证明: ![]() 为定值;
为定值;
(3)当![]() 变化时,直线
变化时,直线![]() 与
与![]() 是否相交于定点?若是,请求出定点的坐标,并给予证明;否则,说明理由.
是否相交于定点?若是,请求出定点的坐标,并给予证明;否则,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com