
科目: 来源: 题型:
【题目】设数列![]()
![]() 是公差不为零等差数列,满足
是公差不为零等差数列,满足![]() ;数列
;数列![]()
![]() 的前
的前![]() 项和为
项和为![]() ,且满足
,且满足![]() .
.
(1)求数列![]() 、
、![]() 的通项公式;
的通项公式;
(2)在![]() 和
和![]() 之间插入1个数
之间插入1个数![]() ,使
,使![]() 成等差数列;在
成等差数列;在![]() 和
和![]() 之间插入2个数
之间插入2个数![]() ,使
,使![]() 成等差数列;……;在
成等差数列;……;在![]() 和
和![]() 之间插入
之间插入![]() 个数
个数![]() ,使
,使![]() 成等差数列,
成等差数列,
(i)求![]() ;
;
(ii)是否存在正整数![]() ,使
,使![]() 成立?若存在,求出所有的正整数对
成立?若存在,求出所有的正整数对![]() ;若不存在,请说明理由.
;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】设![]() 为实数,已知函数
为实数,已知函数![]() 的导函数为
的导函数为![]() ,且
,且![]() .
.
(1)求![]() 的值;
的值;
(2)设![]() 为实数,若对于任意
为实数,若对于任意![]() ,不等式
,不等式![]() 恒成立,且存在唯一的实数
恒成立,且存在唯一的实数![]() 使得
使得![]() 成立,求
成立,求![]() 的值;
的值;
(3)是否存在负数![]() ,使得
,使得![]() 是曲线
是曲线![]() 的切线.若存在,求出
的切线.若存在,求出![]() 的所有值:若不存在,请说明理由.
的所有值:若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
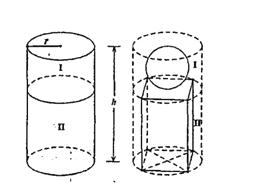
【题目】某人利用一根原木制作一件手工作品,该作品由一个球体和一个正四棱柱组成,假定原 木为圆柱体(如图1),底面半径为![]() ,高为
,高为![]() ,制作要求如下:首先需将原木切割为两部分(分别称为第I圆柱和第II圆柱),要求切面与原木的上下底面平行(不考虑损耗) 然后将第I圆柱切割为一个球体,要求体积最大,将第II圆柱切割为一个正四棱柱,要求正四棱柱的上下底面分别为第II圆柱上下底面圆的内接正方形.
,制作要求如下:首先需将原木切割为两部分(分别称为第I圆柱和第II圆柱),要求切面与原木的上下底面平行(不考虑损耗) 然后将第I圆柱切割为一个球体,要求体积最大,将第II圆柱切割为一个正四棱柱,要求正四棱柱的上下底面分别为第II圆柱上下底面圆的内接正方形.
(1)当![]() 时,若第I圆柱和第II圆柱的体积相等,求该手王作品的体积;
时,若第I圆柱和第II圆柱的体积相等,求该手王作品的体积;
(2)对于给定的![]() 和
和![]() ,求手工作品体积的最大值.
,求手工作品体积的最大值.
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系![]() 中,
中,![]() 的离心率为
的离心率为![]() ,且点
,且点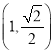 在此椭圆上.
在此椭圆上.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设直线![]() 与圆
与圆![]() 相切于第一象限内的点
相切于第一象限内的点![]() ,且
,且![]() 与椭圆
与椭圆![]() 交于
交于![]() .两点.若
.两点.若![]() 的面积为
的面积为![]() ,求直线
,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目: 来源: 题型:
【题目】进位制是人们为了计数和运算方便而约定的计数系统,“满几进一”就是几进制,不同进制之间可以相互转化,例如把十进制的89转化为二进制,根据二进制数“满二进一”的原则,可以用2连续去除89得商,然后取余数,具体计算方法如下:
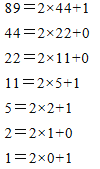
把以上各步所得余数从下到上排列,得到89=1011001(2)这种算法叫做“除二取余法”,上述方法也可以推广为把十进制数化为k进制数的方法,称为“除k取余法”,那么用“除k取余法”把89化为七进制数为_.
查看答案和解析>>
科目: 来源: 题型:
【题目】2019年1月3日嫦娥四号探测器成功实现人类历史上首次月球背面软着陆,我国航天事业取得又一重大成就,实现月球背面软着陆需要解决的一个关键技术问题是地面与探测器的通讯联系.为解决这个问题,发射了嫦娥四号中继星“鹊桥”,鹊桥沿着围绕地月拉格朗日![]() 点的轨道运行.
点的轨道运行.![]() 点是平衡点,位于地月连线的延长线上.设地球质量为M1,月球质量为M2,地月距离为R,
点是平衡点,位于地月连线的延长线上.设地球质量为M1,月球质量为M2,地月距离为R,![]() 点到月球的距离为r,根据牛顿运动定律和万有引力定律,r满足方程:
点到月球的距离为r,根据牛顿运动定律和万有引力定律,r满足方程:
![]() .
.
设![]() ,由于
,由于![]() 的值很小,因此在近似计算中
的值很小,因此在近似计算中![]() ,则r的近似值为
,则r的近似值为
A.  B.
B. 
C.  D.
D. 
查看答案和解析>>
科目: 来源: 题型:
【题目】三国时代吴国数学家赵爽所注《周髀算经》中给出了勾股定理的绝妙证明.下面是赵爽的弦图及注文,弦图是一个以勾股形之弦为边的正方形,其面积称为弦实.图中包含四个全等的勾股形及一个小正方形,分别涂成红(朱)色及黄色,其面积称为朱实、黄实,利用![]() ,化简,得
,化简,得![]() .设勾股形中勾股比为
.设勾股形中勾股比为![]() ,若向弦图内随机抛掷
,若向弦图内随机抛掷![]() 颗图钉(大小忽略不计),则落在黄色图形内的图钉数大约为( )
颗图钉(大小忽略不计),则落在黄色图形内的图钉数大约为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】2016年1月14日,国防科工局宣布,嫦娥四号任务已经通过了探月工程重大专项领导小组审议通过,正式开始实施.如图所示,假设“嫦娥四号”卫星将沿地月转移轨道飞向月球后,在月球附近一点P变轨进入以月球球心F为一个焦点的椭圆轨道Ⅰ绕月飞行,之后卫星在P点第二次变轨进入仍以F为一个焦点的椭圆轨道Ⅱ绕月飞行.若用![]() 和
和![]() 分别表示椭圆轨道Ⅰ和Ⅱ的焦距,用
分别表示椭圆轨道Ⅰ和Ⅱ的焦距,用![]() 和
和![]() 分别表示椭圆轨道Ⅰ和Ⅱ的长轴长,给出下列式子:①
分别表示椭圆轨道Ⅰ和Ⅱ的长轴长,给出下列式子:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .其中正确式子的序号是( )
.其中正确式子的序号是( )

A.①③B.①④C.②③D.②④
查看答案和解析>>
科目: 来源: 题型:
【题目】狄利克雷函数是高等数学中的一个典型函数,若![]() ,则称
,则称![]() 为狄利克雷函数.对于狄利克雷函数
为狄利克雷函数.对于狄利克雷函数![]() ,给出下面4个命题:①对任意
,给出下面4个命题:①对任意![]() ,都有
,都有![]() ;②对任意
;②对任意![]() ,都有
,都有![]() ;③对任意
;③对任意![]() ,都有
,都有![]() ,
, ![]() ;④对任意
;④对任意![]() ,都有
,都有![]() .其中所有真命题的序号是( )
.其中所有真命题的序号是( )
A. ①④ B. ②③ C. ①②③ D. ①③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com