
科目: 来源: 题型:
【题目】明初出现了一大批杰出的骑兵将领,比如徐达、常遇春、李文忠、蓝玉和朱棣.明初骑兵军团击败了不可一世的蒙古骑兵,是当时世界上最强骑兵军团.假设在明军与元军的某次战役中,明军有8位将领,善用骑兵的将领有5人;元军有8位将领,善用骑兵的有4人.
(1)现从明军将领中随机选取4名将领,求至多有3名是善用骑兵的将领的概率;
(2)在明军和元军的将领中各随机选取2人,![]() 为善用骑兵的将领的人数,写出
为善用骑兵的将领的人数,写出![]() 的分布列,并求
的分布列,并求![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】定义在![]() 上的偶函数
上的偶函数![]() 满足
满足![]() ,且
,且![]() ,当
,当![]() 时,
时,![]() .已知方程
.已知方程![]() 在区间
在区间![]() 上所有的实数根之和为
上所有的实数根之和为![]() .将函数
.将函数![]() 的图象向右平移
的图象向右平移![]() 个单位长度,得到函数
个单位长度,得到函数![]() 的图象,则
的图象,则![]() __________,
__________,![]() __________.
__________.
查看答案和解析>>
科目: 来源: 题型:
【题目】椭圆![]() 的左、右顶点分别为
的左、右顶点分别为![]() ,上、下顶点分别为
,上、下顶点分别为![]() ,左、右焦点分别为
,左、右焦点分别为![]() ,
,![]() ,离心率为
,离心率为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)过右焦点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 两点,试探究在
两点,试探究在![]() 轴上是否存在定点
轴上是否存在定点![]() ,使得可
,使得可![]() 为定值?若存在,求出点
为定值?若存在,求出点![]() 的坐标,若不存在,请说明理由?
的坐标,若不存在,请说明理由?
查看答案和解析>>
科目: 来源: 题型:
【题目】一个不透明的盒子中关有蝴蝶、蜜蜂和蜻蜓三种昆虫共11只,现在盒子上开一小孔,每次只能飞出1只昆虫(假设任意1只昆虫等可能地飞出).若有2只昆虫先后任意飞出(不考虑顺序),则飞出的是蝴蝶或蜻蜓的概率是![]() .
.
(1)求盒子中蜜蜂有几只;
(2)若从盒子中先后任意飞出3只昆虫(不考虑顺序),记飞出蜜蜂的只数为X,求随机变量X的分布列与数学期望E(X).
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数f(x)=|2x﹣a|,g(x)=x+1.
(1)若a=1,求不等式f(x)≤1的解集;
(2)对任意的x∈R,f(x)+|g(x)|≥a2+2a(a>0)恒成立,求实数a的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知直线![]() 过椭圆
过椭圆![]() 的右焦点
的右焦点![]() ,抛物线
,抛物线![]() 的焦点为椭圆
的焦点为椭圆![]() 的上顶点,且
的上顶点,且![]() 交椭圆
交椭圆![]() 于
于![]() 两点,点
两点,点![]() 在直线
在直线![]() 上的射影依次为
上的射影依次为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)若直线![]() 交
交![]() 轴于点
轴于点![]() ,且
,且![]() ,当
,当![]() 变化时,证明:
变化时,证明: ![]() 为定值;
为定值;
(3)当![]() 变化时,直线
变化时,直线![]() 与
与![]() 是否相交于定点?若是,请求出定点的坐标,并给予证明;否则,说明理由.
是否相交于定点?若是,请求出定点的坐标,并给予证明;否则,说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】某种商品在50个不同地区的零售价格全部介于13元与18元之间,将各地价格按如下方式分成五组:第一组![]() ,第二组
,第二组![]() ,……,第五组
,……,第五组![]() .如图是按上述分组方法得到的频率分布直方图.
.如图是按上述分组方法得到的频率分布直方图.
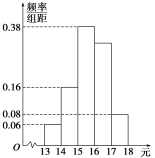
(1)求价格落在![]() 内的地区数;
内的地区数;
(2)借助频率分布直方图,估计该商品价格的中位数(精确到0.1);
(3)现从![]() ,
,![]() 这两组的全部样本数据中,随机选取两个地区的零售价格,记为
这两组的全部样本数据中,随机选取两个地区的零售价格,记为![]() ,
,![]() ,求事件“
,求事件“![]() ”的概率.
”的概率.
查看答案和解析>>
科目: 来源: 题型:
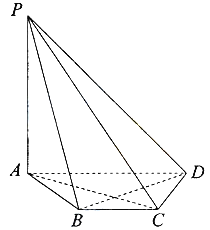
【题目】如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是等腰梯形,AD∥BC,AC⊥BD.
(Ⅰ)证明:BD⊥PC;
(Ⅱ)若AD=4,BC=2,直线PD与平面PAC所成的角为30°,求四棱锥P-ABCD的体积.
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为 ,其中
,其中![]() 为参数,
为参数,![]() .在以坐标原点
.在以坐标原点![]() 为极点,轴的正半轴为极轴的极坐标系中,点
为极点,轴的正半轴为极轴的极坐标系中,点![]() 的极坐标为
的极坐标为![]() ,直线
,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的直角坐标方程与曲线
的直角坐标方程与曲线![]() 的普通方程;
的普通方程;
(2)若![]() 是曲线
是曲线![]() 上的动点,
上的动点,![]() 为线段
为线段![]() 的中点.求点
的中点.求点![]() 到直线
到直线![]() 的距离的最大值.
的距离的最大值.
查看答案和解析>>
科目: 来源: 题型:
【题目】在直角坐标系![]() 中,以坐标原点
中,以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,直线
,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).
为参数).
(1)求![]() 与
与![]() 的交点的直角坐标;
的交点的直角坐标;
(2)求![]() 上的点到直线
上的点到直线![]() 的距离的最大值.
的距离的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com