
科目: 来源: 题型:
【题目】设函数y=f(x)的定义域为D,若对任意的x1∈D,总存在x2∈D,使得f(x1)f(x2)=1,则称函数f(x)具有性质M.下列结论:①函数y=x3﹣x具有性质M;②函数y=3x+5x具有性质M;③若函数y=log8(x+2),x∈[0,t]时具有性质M,则t=510;④若y![]() 具有性质M,则a=5.其中正确结论的序号是_____.
具有性质M,则a=5.其中正确结论的序号是_____.
查看答案和解析>>
科目: 来源: 题型:
【题目】设曲线E的方程为![]() 1,动点A(m,n),B(﹣m,n),C(﹣m,﹣n),D(m,﹣n)在E上,对于结论:①四边形ABCD的面积的最小值为48;②四边形ABCD外接圆的面积的最小值为25π.下面说法正确的是( )
1,动点A(m,n),B(﹣m,n),C(﹣m,﹣n),D(m,﹣n)在E上,对于结论:①四边形ABCD的面积的最小值为48;②四边形ABCD外接圆的面积的最小值为25π.下面说法正确的是( )
A.①错,②对B.①对,②错C.①②都错D.①②都对
查看答案和解析>>
科目: 来源: 题型:
【题目】某高校健康社团为调查本校大学生每周运动的时长,随机选取了80名学生,调查他们每周运动的总时长(单位:小时),按照![]()
![]()
![]()
![]()
![]()
![]() 共6组进行统计,得到男生、女生每周运动的时长的统计如下(表1、2),规定每周运动15小时以上(含15小时)的称为“运动合格者”,其中每周运动25小时以上(含25小时)的称为“运动达人”.
共6组进行统计,得到男生、女生每周运动的时长的统计如下(表1、2),规定每周运动15小时以上(含15小时)的称为“运动合格者”,其中每周运动25小时以上(含25小时)的称为“运动达人”.
表1:男生
时长 |
|
|
|
|
|
|
人数 | 2 | 8 | 16 | 8 | 4 | 2 |
表2:女生
时长 |
|
|
|
|
|
|
人数 | 0 | 4 | 12 | 12 | 8 | 4 |
(1)从每周运动时长不小于20小时的男生中随机选取2人,求选到“运动达人”的概率;
(2)根据题目条件,完成下面![]() 列联表,并判断能否有99%的把握认为本校大学生是否为“运动合格者”与性别有关.
列联表,并判断能否有99%的把握认为本校大学生是否为“运动合格者”与性别有关.
每周运动的时长小于15小时 | 每周运动的时长不小于15小时 | 总计 | |
男生 | |||
女生 | |||
总计 | |||
参考公式: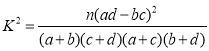 ,其中
,其中![]() .
.
参考数据:
| 0.40 | 0.25 | 0.10 | 0.010 |
| 0.708 | 1.323 | 2.706 | 6.635 |
查看答案和解析>>
科目: 来源: 题型:
【题目】某工厂为提高生产效率,开展技术创新活动,提出了完成某项生产任务的两种新的生产方式.为比较两种生产方式的效率,选取40名工人,将他们随机分成两组,每组20人,第一组工人用第一种生产方式,第二组工人用第二种生产方式.根据工人完成生产任务的工作时间(单位:min)绘制了如下茎叶图:

(1)根据茎叶图判断哪种生产方式的效率更高?并说明理由;
(2)求40名工人完成生产任务所需时间的中位数![]() ,并将完成生产任务所需时间超过
,并将完成生产任务所需时间超过![]() 和不超过
和不超过![]() 的工人数填入下面的列联表:
的工人数填入下面的列联表:
超过 | 不超过 | |
第一种生产方式 | ||
第二种生产方式 |
(3)根据(2)中的列联表,能否有99%的把握认为两种生产方式的效率有差异?
附:![]() ,
,
|
|
|
|
|
|
|
|
查看答案和解析>>
科目: 来源: 题型:
【题目】某市2010年4月1日—4月30日对空气污染指数的监测数据如(主要污染物为可吸入颗粒物):61,76,70,56,81,91,92,91,75,81,88,67,101,103,95,91,77,86,83,82,82,64,79,86,85,75,71,49,45.
样本频率分布表:
分组 | 频数 | 频率 |
[41,51) | 2 | |
[51,61) | 1 | |
[61,71) | 4 | |
[71,81) | 6 | |
[81,91) | 10 | |
[91,101) | ||
[101,111) | 2 |
(1) 完成频率分布表;
(2)作出频率分布直方图;
(3)根据国家标准,污染指数在0~50之间时,空气质量为优:在51~100之间时,为良;在101~150之间时,为轻微污染;在151~200之间时,为轻度污染.请你依据所给数据和上述标准,对该市的空气质量给出一个简短评价.
查看答案和解析>>
科目: 来源: 题型:
【题目】某良种培育基地正在培育一种小麦新品种A.将其与原有的一个优良品种B进行对照试验.两种小麦各种植了25亩,所得亩产数据(单位:千克)如下:
品种A:357,359,367,368,375,388,392,399,400,405,412, 414,415,421,423,423,427,430,430,434,443,445,445,451,454
品种B:363,371,374,383,385,386,391,392,394,394,395, 397,397,400,401,401,403,406,407,410,412,415,416,422,430
(1)作出茎叶图;
(2)通过观察茎叶图,对品种A与B的亩产量及其稳定性进行比较,写出统计结论.
查看答案和解析>>
科目: 来源: 题型:
【题目】从某企业生产的某种产品中抽取100件,测量这些产品的一项质量指标值,由测量表得如下频数分布表:
质量指标值分组 | [75,85) | [85,95) | [95,105) | [105,115) | [115,125) |
频数 | 6 | 26 | 38 | 22 | 8 |
(I)在答题卡上作出这些数据的频率分布直方图:
(II)估计这种产品质量指标值的平均数及方差(同一组中的数据用该组区间的中点值作代表);
(III)根据以上抽样调查数据,能否认为该企业生产的这种产品符合“质量指标值不低于95的产品至少要占全部产品的80%”的规定?
查看答案和解析>>
科目: 来源: 题型:
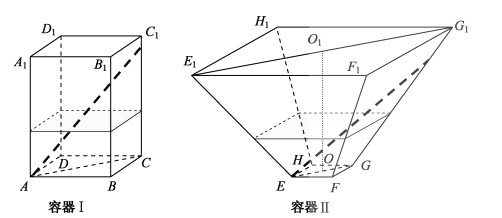
【题目】如图,水平放置的正四棱柱形玻璃容器Ⅰ和正四棱台形玻璃容器Ⅱ的高均为32cm,容器Ⅰ的底面对角线AC的长为10![]() cm,容器Ⅱ的两底面对角线EG,E1G1的长分别为14cm和62cm. 分别在容器Ⅰ和容器Ⅱ中注入水,水深均为12cm. 现有一根玻璃棒l,其长度为40cm.(容器厚度、玻璃棒粗细均忽略不计)
cm,容器Ⅱ的两底面对角线EG,E1G1的长分别为14cm和62cm. 分别在容器Ⅰ和容器Ⅱ中注入水,水深均为12cm. 现有一根玻璃棒l,其长度为40cm.(容器厚度、玻璃棒粗细均忽略不计)
(1)将l放在容器Ⅰ中,l的一端置于点A处,另一端置于侧棱CC1上,求l没入水中部分的长度;
(2)将l放在容器Ⅱ中,l的一端置于点E处,另一端置于侧棱GG1上,求l没入水中部分的长度.
查看答案和解析>>
科目: 来源: 题型:
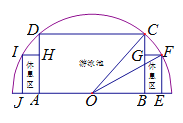
【题目】如图,有一块半圆形空地,开发商计划建造一个矩形游泳池![]() 及左右两侧两个大小相同的矩形休息区,其中半圆的圆心为
及左右两侧两个大小相同的矩形休息区,其中半圆的圆心为![]() ,半径为
,半径为![]() ,矩形
,矩形![]() 的一边
的一边![]() 在
在![]() 上,矩形
上,矩形![]() 的一边
的一边![]() 在
在![]() 上,点
上,点![]() 在圆周上,
在圆周上,![]() 在直径上,且
在直径上,且![]() ,设
,设![]() .若每平方米游泳池的造价和休息区造价分别为
.若每平方米游泳池的造价和休息区造价分别为![]() 和
和![]() .
.
(1)记游泳池及休息区的总造价为![]() ,求
,求![]() 的表达式;
的表达式;
(2)为进行投资预算,当![]() 为何值时,总造价最大?并求出总造价的最大值.
为何值时,总造价最大?并求出总造价的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com