
科目: 来源: 题型:
【题目】为考查某种疫苗预防疾病的效果,进行动物实验,得到统计数据如下表:
未发病 | 发病 | 合计 | |
未注射疫苗 | 40 |
|
|
注射疫苗 | 60 |
|
|
合计 | 100 | 100 | 200 |
现从所有试验动物中任取一只,取到“注射疫苗”动物的概率为![]() .
.
(1)求![]() 列联表中的数据
列联表中的数据![]() 的值;
的值;
(2)在图中绘制发病率的条形统计图,并判断疫苗是否有效?
(3)在出错概率不超过![]() 的条件下能否认为疫苗有效?
的条件下能否认为疫苗有效?
附: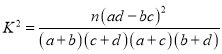 .
.
| 0.05 | 0.01 | 0.005 | 0.001 |
| 3.841 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目: 来源: 题型:
【题目】设椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() 、
、![]() ,上顶点为
,上顶点为![]() ,在
,在![]() 轴负半轴上有一点
轴负半轴上有一点![]() ,满足
,满足![]() 为线段
为线段![]() 的中点,且
的中点,且![]() .
.
(1)求椭圆![]() 的离心率;
的离心率;
(2)若过![]() 、
、![]() 、
、![]() 三点的圆与直线
三点的圆与直线![]() 相切,求椭圆
相切,求椭圆![]() 的方程;
的方程;
(3)在(2)的条件下,过右焦点![]() 作斜率为
作斜率为![]() 的直线与椭圆
的直线与椭圆![]() 交于
交于![]() 、
、![]() 两点,在
两点,在![]() 轴上是否存在点
轴上是否存在点![]() 使得以
使得以![]() 、
、![]() 为邻边的平行四边形是菱形?如果存在,求出
为邻边的平行四边形是菱形?如果存在,求出![]() 的取值范围,若不存在,请说明理由.
的取值范围,若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】(本小题满分12分)如图,三棱柱ABC-A1B1C1中,CA=CB,AB=A A1,∠BA A1=60°.
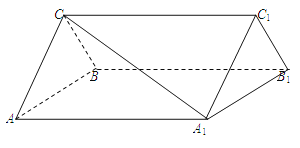
(Ⅰ)证明AB⊥A1C;
(Ⅱ)若平面ABC⊥平面AA1B1B,AB=CB,求直线A1C 与平面BB1C1C所成角的正弦值。
查看答案和解析>>
科目: 来源: 题型:
【题目】某超市从![]() 年甲、乙两种酸奶的日销售量(单位:箱)的数据中分别随机抽取
年甲、乙两种酸奶的日销售量(单位:箱)的数据中分别随机抽取![]() 个,并按
个,并按![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 分组,得到频率分布直方图如图,假设甲、乙两种酸奶独立销售且日销售量相互独立.
分组,得到频率分布直方图如图,假设甲、乙两种酸奶独立销售且日销售量相互独立.
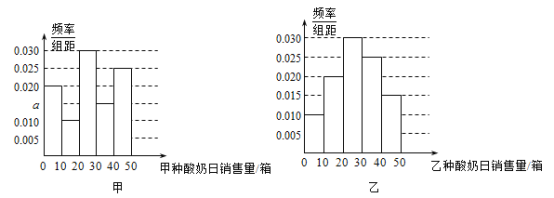
(1)写出频率分布直方图甲中的![]() 的值;记甲种酸奶与乙种酸奶日销售量(单位:箱)的方差分别为
的值;记甲种酸奶与乙种酸奶日销售量(单位:箱)的方差分别为![]() 、
、![]() ,试比较
,试比较![]() 与
与![]() 的大小;(只需写出结论)
的大小;(只需写出结论)
(2)估计在未来的某一天里,甲、乙两种酸奶的销售量恰有一个高于![]() 箱且另一个不高于
箱且另一个不高于![]() 箱的概率;
箱的概率;
(3)设![]() 表示在未来
表示在未来![]() 天内甲种酸奶的日销售量不高于
天内甲种酸奶的日销售量不高于![]() 箱的天数,以日留住量落入各组的频率为概率,求
箱的天数,以日留住量落入各组的频率为概率,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目: 来源: 题型:
【题目】某商场举行双12有奖促销活动,顾客购买168元的商品后即可抽奖,抽奖方法是:从装有2个红球![]() 和1个白球
和1个白球![]() 的甲箱与装有2个红球
的甲箱与装有2个红球![]() 和1个白球
和1个白球![]() 的乙箱中,各随机摸出1个球,这些球除颜色,标号外都一样.若摸出的2个球颜色相同则中奖,否则不中奖.
的乙箱中,各随机摸出1个球,这些球除颜色,标号外都一样.若摸出的2个球颜色相同则中奖,否则不中奖.
(1)用球的标号列出所有可能的摸出结果;
(2)小明根据经验认为:摸到同色球一般来说更为难得,所以猜测中奖的概率小于不中奖的概率,你认为小明的猜想正确吗?请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆![]() 的左顶点为A1,右焦点为F2,过点F2作垂直于x轴的直线交该椭圆于M、N两点,直线A1M的斜率为
的左顶点为A1,右焦点为F2,过点F2作垂直于x轴的直线交该椭圆于M、N两点,直线A1M的斜率为![]() .
.
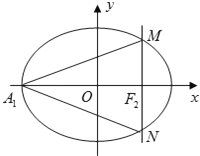
(Ⅰ)求椭圆的离心率;
(Ⅱ)若△A1MN的外接圆在M处的切线与椭圆相交所得弦长为![]() ,求椭圆方程.
,求椭圆方程.
查看答案和解析>>
科目: 来源: 题型:
【题目】在一次期末数学测试中,唐老师任教班级学生的考试得分情况如表所示:
分数区间 |
|
|
|
|
|
人数 | 2 | 8 | 32 | 38 | 20 |
(1)根据上述表格,试估计唐老师所任教班级的学生在本次期末数学测试的平均成绩;
(2)现从成绩在![]() 中按照分数段,采取分层抽样的方法随机抽取5人,再在这5人中随机抽取2人作小题得分分析,求恰有1人的成绩在
中按照分数段,采取分层抽样的方法随机抽取5人,再在这5人中随机抽取2人作小题得分分析,求恰有1人的成绩在![]() 上的概率.
上的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com