
科目: 来源: 题型:
【题目】如图1,在等腰梯形ABCD中,![]() ,
,![]() ,
,![]() ,E为AD的中点.现分别沿BE,EC将△ABE 和△ECD折起,使得平面ABE⊥平面BCE,平面ECD⊥平面BCE,连接AD,如图2.
,E为AD的中点.现分别沿BE,EC将△ABE 和△ECD折起,使得平面ABE⊥平面BCE,平面ECD⊥平面BCE,连接AD,如图2.
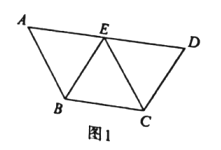
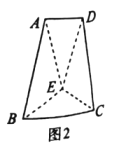
(1)若在平面BCE内存在点G,使得GD∥平面ABE,请问点G的轨迹是什么图形?并说明理由.
(2)求平面AED与平面BCE所成锐二面角的余弦值.
查看答案和解析>>
科目: 来源: 题型:
【题目】某市一所高中为备战即将举行的全市羽毛球比赛,学校决定组织甲、乙两队进行羽毛球对抗赛实战训练.每队四名运动员,并统计了以往多次比赛成绩,按由高到低进行排序分别为第一名、第二名、第三名、第四名.比赛规则为甲、乙两队同名次的运动员进行对抗,每场对抗赛都互不影响,当甲、乙两队的四名队员都进行一次对抗赛后称为一个轮次.按以往多次比赛统计的结果,甲、乙两队同名次进行对抗时,甲队队员获胜的概率分别为![]() ,
,![]() ,
,![]() ,
,![]() .
.
(1)进行一个轮次对抗赛后一共有多少种对抗结果?
(2)计分规则为每次对抗赛获胜一方所在的队得1分,失败一方所在的队得0分,设进行一个轮次对抗赛后甲队所得分数为X,求X的分布列及数学期望.
查看答案和解析>>
科目: 来源: 题型:
【题目】已如椭圆C:![]() 的两个焦点与其中一个顶点构成一个斜边长为4的等腰直角三角形.
的两个焦点与其中一个顶点构成一个斜边长为4的等腰直角三角形.
(1)求椭圆C的标准方程;
(2)设动直线l交椭圆C于P,Q两点,直线OP,OQ的斜率分别为k,k'.若![]() ,求证△OPQ的面积为定值,并求此定值.
,求证△OPQ的面积为定值,并求此定值.
查看答案和解析>>
科目: 来源: 题型:
【题目】将函数![]() 图象上的所有点的横坐标伸长到原来的2倍,再把所得各点向右平移
图象上的所有点的横坐标伸长到原来的2倍,再把所得各点向右平移![]() 个单位长度,最后把所得各点纵坐标扩大到原来的2倍,就得到函数f(x)的图象,则下列说法中正确的个数是( )
个单位长度,最后把所得各点纵坐标扩大到原来的2倍,就得到函数f(x)的图象,则下列说法中正确的个数是( )
①函数f(x)的最小正周期为2π;
②函数f(x)的最大值为2;
③函数f(x)图象的对称轴方程为![]() ;
;
④设x1,x2为方程![]() 的两个不相等的根,则
的两个不相等的根,则![]() 的最小值为
的最小值为![]() .
.
A.1B.2C.3D.4
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数![]() ,其中
,其中![]() 为常数.
为常数.
(1)当![]() 时,解不等式
时,解不等式![]() ;
;
(2)已知![]() 是以2为周期的偶函数,且当
是以2为周期的偶函数,且当![]() 时,有
时,有![]() .若
.若![]() ,且
,且![]() ,求函数
,求函数![]()
![]() 的反函数;
的反函数;
(3)若在![]() 上存在
上存在![]() 个不同的点
个不同的点![]() ,
,![]() ,使得
,使得![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知数列![]() 各项均为正数,
各项均为正数,![]() 为其前
为其前![]() 项的和,且
项的和,且![]() 成等差数列.
成等差数列.
(1)写出![]() 、
、![]() 、
、![]() 的值,并猜想数列
的值,并猜想数列![]() 的通项公式
的通项公式![]() ;
;
(2)证明(1)中的猜想;
(3)设![]() ,
,![]() 为数列
为数列![]() 的前
的前![]() 项和.若对于任意
项和.若对于任意![]() ,都有
,都有![]() ,求实数
,求实数![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】某港口某天0时至24时的水深![]() (米)随时间
(米)随时间![]() (时)变化曲线近似满足如下函数模型
(时)变化曲线近似满足如下函数模型![]() (
(![]() ).若该港口在该天0时至24时内,有且只有3个时刻水深为3米,则该港口该天水最深的时刻不可能为( )
).若该港口在该天0时至24时内,有且只有3个时刻水深为3米,则该港口该天水最深的时刻不可能为( )
A.16时B.17时C.18时D.19时
查看答案和解析>>
科目: 来源: 题型:
【题目】已知正方体![]() ,点
,点![]() 是棱
是棱![]() 的中点,设直线
的中点,设直线![]() 为
为![]() ,直线
,直线![]() 为
为![]() .对于下列两个命题:①过点
.对于下列两个命题:①过点![]() 有且只有一条直线
有且只有一条直线![]() 与
与![]() 、
、![]() 都相交;②过点
都相交;②过点![]() 有且只有一条直线
有且只有一条直线![]() 与
与![]() 、
、![]() 都成
都成![]() 角.以下判断正确的是( )
角.以下判断正确的是( )
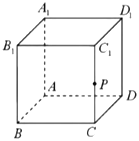
A.①为真命题,②为真命题B.①为真命题,②为假命题
C.①为假命题,②为真命题D.①为假命题,②为假命题
查看答案和解析>>
科目: 来源: 题型:
【题目】近年来,人们支付方式发生巨大转变,使用移动支付购买商品已成为一部分人的消费习惯,某企业为了解该企业员工![]() 两种移动支付方式的使用情况,从全体员工中随机抽取了100人,统计了他们在某个月的消费支出情况,发现样本中
两种移动支付方式的使用情况,从全体员工中随机抽取了100人,统计了他们在某个月的消费支出情况,发现样本中![]() 两种支付方式都没有使用过的有5人;使用了
两种支付方式都没有使用过的有5人;使用了![]() 两种方式支付的员工,支付金额和相应人数分布如下表,依据数据估算:若从该公司随机抽取1名员工,则该员工在该月
两种方式支付的员工,支付金额和相应人数分布如下表,依据数据估算:若从该公司随机抽取1名员工,则该员工在该月![]() 两种支付方式都使用过的概率为_______________
两种支付方式都使用过的概率为_______________
支付金额(元) 支付方式 |
|
| 大于2000 |
使用 | 18人 | 29人 | 23人 |
使用 | 10人 | 24人 | 21人 |
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系xoy中,以坐标原点O为极点,x轴正半轴为极轴建立极坐标系。已知曲线C的极坐标方程为![]() ,过点
,过点![]() 的直线l的参数方程为
的直线l的参数方程为 (为参数),直线l与曲线C交于M、N两点。
(为参数),直线l与曲线C交于M、N两点。
(1)写出直线l的普通方程和曲线C的直角坐标方程:
(2)若![]() 成等比数列,求a的值。
成等比数列,求a的值。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com