
科目: 来源: 题型:
【题目】下列说法正确的是( )
A.在频率分布直方图中,众数左边和右边的直方图的面积相等;
B.为调查高三年级的240名学生完成作业所需的时间,由教务处对高三年级的学生进行編号,从001到240抽取学号最后一位为3的学生进行调查,则这种抽样方法为分层抽样;
C.“![]() ”是“
”是“![]() ”的必要不充分条件;
”的必要不充分条件;
D.命题![]() :“
:“![]() ,使得
,使得![]() ”的否定为:“
”的否定为:“![]() ,均有
,均有![]() ”.
”.
查看答案和解析>>
科目: 来源: 题型:
【题目】一只红玲虫的产卵数![]() 和温度
和温度![]() 有关.现收集了7组观测数据如下表:
有关.现收集了7组观测数据如下表:
温度 | 21 | 23 | 25 | 27 | 29 | 32 | 35 |
产卵数 | 7 | 11 | 21 | 24 | 66 | 115 | 325 |
为了预报一只红玲虫在![]() 时的产卵数,根据表中的数据建立了
时的产卵数,根据表中的数据建立了![]() 与
与![]() 的两个回归模型.模型①:先建立
的两个回归模型.模型①:先建立![]() 与
与![]() 的指数回归方程
的指数回归方程![]() ,然后通过对数变换
,然后通过对数变换![]() ,把指数关系变为
,把指数关系变为![]() 与
与![]() ;模型②:先建立
;模型②:先建立![]() 与
与![]() 的二次回归方程
的二次回归方程![]() ,然后通过变换
,然后通过变换![]() ,把二次关系变为
,把二次关系变为![]() 与
与![]() 的线性回归方程:
的线性回归方程:![]() .
.
(1)分别利用这两个模型,求一只红玲虫在![]() 时产卵数的预测值;
时产卵数的预测值;
(2)你认为用哪个模型得到的预测值更可靠?并说明理由.(参考数据:模型①的残差平方和![]() ,模型①的相关指数
,模型①的相关指数![]() ;模型②的残差平方和
;模型②的残差平方和![]() ,模型②的相关指数
,模型②的相关指数![]() ;
;![]() ,
,![]() ,
,![]() ;
;![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目: 来源: 题型:
【题目】某农场为了提高某品种水稻的产量,进行良种优选,在同一试验田中分两块种植了甲乙两种水稻.为了比较甲乙两种水稻的产量,现从甲乙两种水稻中各随机选取20株成熟水稻.根据每株水稻颗粒的重量(单位:克)绘制了如下茎叶图:
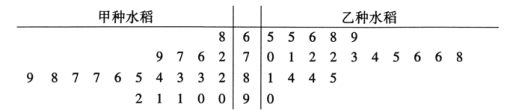
(1)根据茎叶图判断哪种水稻的产量更高?并说明理由;
(2)求40株水稻颗粒重量的中位数![]() ,并将重量超过
,并将重量超过![]() 和不超过
和不超过![]() 的水稻株数填入下面的列联表:
的水稻株数填入下面的列联表:
超过 | 不超过 | |
甲种水稻 | ||
乙种水稻 |
(3)根据(2)中的列联表,能否有![]() 的把握认为两种水稻的产量有差异?附:
的把握认为两种水稻的产量有差异?附: ;
;
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目: 来源: 题型:
【题目】某花圃为提高某品种花苗质量,开展技术创新活动,在![]() 实验地分别用甲、乙方法培育该品种花苗.为观测其生长情况,分别在实验地随机抽取各50株,对每株进行综合评分,将每株所得的综合评分制成如图所示的频率分布直方图,记综合评分为80及以上的花苗为优质花苗.
实验地分别用甲、乙方法培育该品种花苗.为观测其生长情况,分别在实验地随机抽取各50株,对每株进行综合评分,将每株所得的综合评分制成如图所示的频率分布直方图,记综合评分为80及以上的花苗为优质花苗.

(1)求图中![]() 的值,并估计该品种花苗综合评分的平均数(同一组中的数据用该组区间的中点值为代表);
的值,并估计该品种花苗综合评分的平均数(同一组中的数据用该组区间的中点值为代表);
(2)填写下面的列联表,并判断是否有99%的把握认为优质花苗与培驻外方法有关.
优质花苗 | 非优质花苗 | 合计 | |
甲培育法 | 20 | ||
乙培育法 | 10 | ||
合计 |
附:下面的临界值表仅供参考.
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
(参考公式: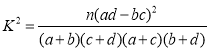 ,其中
,其中![]() )
)
查看答案和解析>>
科目: 来源: 题型:
【题目】如图所示的几何体中,![]() 为直三棱柱,四边形
为直三棱柱,四边形![]() 为平行四边形,
为平行四边形,![]() ,
,![]() ,
,![]() .
.

(1)证明:![]() 四点共面,且
四点共面,且![]() ;
;
(2)若![]() ,点
,点![]() 是
是![]() 上一点,求四棱锥
上一点,求四棱锥![]() 的体积,并判断点
的体积,并判断点![]() 到平面
到平面![]() 的距离是否为定值?请说明理由.
的距离是否为定值?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com