
科目: 来源: 题型:
【题目】端午假期即将到来,永辉超市举办“浓情端午高考加油”有奖促销活动,凡持高考准考证考生及家长在端年节期间消费每超过600元(含600元),均可抽奖一次,抽奖箱里有10个形状、大小完全相同的小球(其中红球有3个,黑球有7个),抽奖方案设置两种,顾客自行选择其中的一种方案.

方案一:
从抽奖箱中,一次性摸出3个球,其中奖规则为:若摸到3个红球,享受免单优惠;若摸出2个红球则打6折,若摸出1个红球,则打7折;若没摸出红球,则不打折.
方案二:
从抽奖箱中,有放回每次摸取1球,连摸3次,每摸到1次红球,立减200元.每次摸取1球,连摸3次,每摸到1次
(1)若小南、小开均分别消费了600元,且均选择抽奖方案一,试求他们均享受免单优惠的概率;
(2)若小杰消费恰好满1000元,试比较说明小杰选择哪一种抽奖方案更合算?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在直角坐标系![]() 中,椭圆
中,椭圆![]() 的上焦点为
的上焦点为![]() ,椭圆
,椭圆![]() 的离心率为
的离心率为![]() ,且过点
,且过点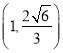 .
.
(1)求椭圆![]() 的方程.
的方程.
(2)设过椭圆![]() 的上顶点
的上顶点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于点
交于点![]() (
(![]() 不在
不在![]() 轴上),垂直于
轴上),垂直于![]() 的直线与
的直线与![]() 交于点
交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,若
,若![]() ,且
,且![]() ,求直线
,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目: 来源: 题型:
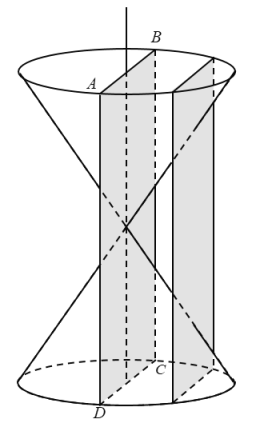
【题目】古希腊数学家阿波罗尼奥斯在他的著作《圆锥曲线论》中记载了用平面切制圆锥得到圆锥曲线的方法.如图,将两个完全相同的圆锥对顶放置(两圆锥的轴重合),已知两个圆锥的底面半径为1,母线长均为![]() ,记过圆锥轴的平面ABCD为平面
,记过圆锥轴的平面ABCD为平面![]() (
(![]() 与两个圆锥面的交线为AC、BD),用平行于
与两个圆锥面的交线为AC、BD),用平行于![]() 的平面截圆锥,该平面与两个圆锥侧面的截线即为双曲线E的一部分,且双曲线E的两条渐近线分别平行于AC、BD,则双曲线E的离心率为( )
的平面截圆锥,该平面与两个圆锥侧面的截线即为双曲线E的一部分,且双曲线E的两条渐近线分别平行于AC、BD,则双曲线E的离心率为( )
A.![]() B.
B.![]() C.
C.![]() D.2
D.2
查看答案和解析>>
科目: 来源: 题型:
【题目】已知动点P到点![]() 的距离与它到直线l:
的距离与它到直线l:![]() 的距离d的比值为
的距离d的比值为![]() ,设动点P形成的轨迹为曲线C.
,设动点P形成的轨迹为曲线C.
(Ⅰ)求曲线C的方程;
(Ⅱ)过点![]() 的直线与曲线C交于A,B两点,设
的直线与曲线C交于A,B两点,设![]() ,
,![]() ,过A点作
,过A点作![]() ,垂足为
,垂足为![]() ,过B点作
,过B点作![]() ,垂足为
,垂足为![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】为庆祝建国70周年,校园文化节举行有奖答题活动,现有A,B两种题型,从A类题型中抽取1道,从B类题型中抽取2道回答,答对3道题获新华书店面值为15元的图书代金券,答对2道题获面值为10元的图书代金券,答对1道题获面值为5元的图书代金券,没有答对获面值为1元的图书代金券(作为鼓励).甲同学参加此活动答对A类题的概率为![]() ,答对B类题的概率为
,答对B类题的概率为![]() .
.
(Ⅰ)求甲答对1道题的概率;
(Ⅱ)设甲参加一次活动所获图书代金券的面值为随机变量X,求X的分布列和数学期望.
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为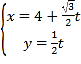 (
(![]() 为参数).以坐标原点为极点,
为参数).以坐标原点为极点,![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]()
(1)在曲线![]() 上任取一点
上任取一点![]() ,连接
,连接![]() ,在射线
,在射线![]() 上取一点
上取一点![]() ,使
,使![]() ,求
,求![]() 点轨迹的极坐标方程;
点轨迹的极坐标方程;
(2)在曲线![]() 上任取一点
上任取一点![]() ,在曲线
,在曲线![]() 上任取一点
上任取一点![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目: 来源: 题型:
【题目】我国历法中将一年分为春、夏、秋、冬四个季节,每个季节有六个节气,如夏季包含立夏、小满、芒种、夏至、小暑以及大暑.某美术学院甲、乙、丙、丁四位同学接到绘制二十四节气的彩绘任务,现四位同学抽签确定各自完成哪个季节中的六幅彩绘,在制签及抽签公平的前提下,甲没有抽到绘制春季六幅彩绘任务且乙没有抽到绘制夏季六幅彩绘任务的概率为_________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com