
科目: 来源: 题型:
【题目】已知椭圆![]() 的两个焦点为
的两个焦点为![]() 、
、![]() ,
,![]() 是
是![]() 与
与![]() 的等差中项,其中
的等差中项,其中![]() 、
、![]() 、
、![]() 都是正数,过点
都是正数,过点![]() 和
和![]() 的直线与原点的距离为
的直线与原点的距离为![]() .
.
(1)求椭圆的方程;
(2)点![]() 是椭圆上一动点,定点
是椭圆上一动点,定点![]() ,求△
,求△![]() 面积的最大值;
面积的最大值;
(3)已知定点![]() ,直线
,直线![]() 与椭圆交于
与椭圆交于![]() 、
、![]() 相异两点.证明:对任意的
相异两点.证明:对任意的![]() ,都存在实数
,都存在实数![]() ,使得以线段
,使得以线段![]() 为直径的圆过
为直径的圆过![]() 点.
点.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知![]() ,
,![]() 为两非零有理数列(即对任意的
为两非零有理数列(即对任意的![]() ,
,![]() 均为有理数),
均为有理数),![]() 为一无理数列(即对任意的
为一无理数列(即对任意的![]() ,
,![]() 为无理数).
为无理数).
(1)已知![]() ,并且
,并且![]() 对任意的
对任意的![]() 恒成立,试求
恒成立,试求![]() 的通项公式.
的通项公式.
(2)若![]() 为有理数列,试证明:对任意的
为有理数列,试证明:对任意的![]() ,
,![]() 恒成立的充要条件为
恒成立的充要条件为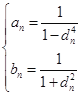 .
.
(3)已知![]() ,
,![]() ,对任意的
,对任意的![]() ,
,![]() 恒成立,试计算
恒成立,试计算![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图放置的边长为1的正方形![]() 沿
沿![]() 轴滚动(向右为顺时针,向左为逆时针).设顶点
轴滚动(向右为顺时针,向左为逆时针).设顶点![]() 的轨迹方程是
的轨迹方程是![]() ,则关于
,则关于![]() 的最小正周期
的最小正周期![]() 及
及![]() 在其两个相邻零点间的图像与x轴所围区域的面积S的正确结论是( )
在其两个相邻零点间的图像与x轴所围区域的面积S的正确结论是( )
![]()
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】有下列四个命题:(1)一定存在直线![]() ,使函数
,使函数![]() 的图像与函数
的图像与函数![]() 的图像关于直线
的图像关于直线![]() 对称;(2)不等式:
对称;(2)不等式:![]() 的解集为
的解集为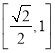 ;(3)已知数列
;(3)已知数列![]() 的前
的前![]() 项和为
项和为![]() ,
,![]() ,则数列
,则数列![]() 一定是等比数列;(4)过抛物线
一定是等比数列;(4)过抛物线![]() 上的任意一点
上的任意一点![]() 的切线方程一定可以表示为
的切线方程一定可以表示为![]() .则正确命题的序号为_________________.
.则正确命题的序号为_________________.
查看答案和解析>>
科目: 来源: 题型:
【题目】某人某天的工作是:驾车从![]() 地出发,到
地出发,到![]() 两地办事,最后返回
两地办事,最后返回![]() 地,
地,![]() 三地之间各路段行驶时间及当天降水概率如表:
三地之间各路段行驶时间及当天降水概率如表:
路段 | 正常行驶所需时间(小时) | 上午降水概率 | 下午降水概率 |
| 2 | 0.3 | 0.6 |
| 2 | 0.2 | 0.7 |
| 3 | 0.3 | 0.9 |
若在某路段遇到降水,则在该路段行驶的时间需延长1小时,现有如下两个方案:
方案甲:上午从![]() 地出发到
地出发到![]() 地办事,然后到达
地办事,然后到达![]() 地,下午在
地,下午在![]() 地办事后返回
地办事后返回![]() 地;
地;
方案乙:上午从![]() 地出发到
地出发到![]() 地办事,下午从
地办事,下午从![]() 地出发到达
地出发到达![]() 地, 办事后返回
地, 办事后返回![]() 地.
地.
(1)设此人8点从![]() 地出发,在各地办事及午餐的累积时间为2小时.且采用方案甲,求他当日18点或18点之前能返回
地出发,在各地办事及午餐的累积时间为2小时.且采用方案甲,求他当日18点或18点之前能返回![]() 地的概率;
地的概率;
(2)甲、乙两个方案中,哪个方案有利于办完事后能更早返回![]() 地?
地?
查看答案和解析>>
科目: 来源: 题型:
【题目】某部门共有4名员工, 某次活动期间, 周六、 周日的上午、 下午各需要安排一名员工值班,若规定同一天的两个值班岗位不能安排给同一名员工, 则该活动值班岗位的不同安排方式共有( )
A.120种B.132种C.144种D.156种
查看答案和解析>>
科目: 来源: 题型:
【题目】某次考试后,对全班同学的数学成绩进行整理,得到表:
分数段 |
|
|
|
|
人数 | 5 | 15 | 20 | 10 |
将以上数据绘制成频率分布直方图后,可估计出本次考试成绩的中位数是__________.
查看答案和解析>>
科目: 来源: 题型:
【题目】在开展学习强国的活动中,某校高三数学教师成立了党员和非党员两个学习组,其中党员学习组有4名男教师、1名女教师,非党员学习组有2名男教师、2名女教师,高三数学组计划从两个学习组中随机各选2名教师参加学校的挑战答题比赛.
(1)求选出的4名选手中恰好有一名女教师的选派方法数;
(2)记X为选出的4名选手中女教师的人数,求X的概率分布和数学期望.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知数列![]() 和
和![]() 都是等差数列,
都是等差数列,![]() .数列
.数列![]() 满足
满足![]() .
.
(1)求![]() 的通项公式;
的通项公式;
(2)证明:![]() 是等比数列;
是等比数列;
(3)是否存在首项为1,公比为q的等比数列![]() ,使得对任意
,使得对任意![]() ,都有
,都有![]() 成立?若存在,求出q的取值范围;若不存在,请说明理由.
成立?若存在,求出q的取值范围;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com