
科目: 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为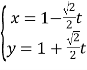 (
(![]() 为参数),以坐标原点为极点,以
为参数),以坐标原点为极点,以![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的普通方程与曲线
的普通方程与曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若![]() 与
与![]() 交于
交于![]() 两点,点
两点,点![]() 的极坐标为
的极坐标为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】2019年庆祝中华人民共和国成立70周年阅兵式彰显了中华民族从站起来、富起来迈向强起来的雄心壮志.阅兵式规模之大、类型之全均创历史之最,编组之新、要素之全彰显强军成就.装备方阵堪称“强军利刃”“强国之盾”,见证着人民军队迈向世界一流军队的坚定步伐.此次大阅兵不仅得到了全中国人的关注,还得到了无数外国人的关注.某单位有6位外国人,其中关注此次大阅兵的有5位,若从这6位外国人中任意选取2位做一次采访,则被采访者都关注了此次大阅兵的概率为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】设函数![]() 的图象在
的图象在![]() 处取得极值4.
处取得极值4.
(1)求函数![]() 的单调区间;
的单调区间;
(2)对于函数![]() ,若存在两个不等正数
,若存在两个不等正数![]() ,
,![]() ,当
,当![]() 时,函数
时,函数![]() 的值域是
的值域是![]() ,则把区间
,则把区间![]() 叫函数
叫函数![]() 的“正保值区间”.问函数
的“正保值区间”.问函数![]() 是否存在“正保值区间”,若存在,求出所有的“正保值区间”;若不存在,请说明理由.
是否存在“正保值区间”,若存在,求出所有的“正保值区间”;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数![]()
![]() 在区间
在区间![]() 上的最大值为9,最小值为1,记
上的最大值为9,最小值为1,记![]() ;
;
(1)求实数![]()
![]() 的值;
的值;
(2)若不等式![]() 成立,求实数
成立,求实数![]() 的取值范围;
的取值范围;
(3)定义在![]() 上的函数
上的函数![]() ,设
,设![]() ,其中
,其中![]()
![]()
![]()
![]() 将区间
将区间![]() 任意划分成
任意划分成![]() 个小区间,如果存在一个常数
个小区间,如果存在一个常数![]() ,使得和式
,使得和式![]() 恒成立,则称函数
恒成立,则称函数![]() 为在
为在![]() 上的有界变差函数,试判断函数
上的有界变差函数,试判断函数![]() 是否为在
是否为在![]() 上的有界变差函数?若是,求
上的有界变差函数?若是,求![]() 的最小值;若不是,请说明理由.
的最小值;若不是,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】某工厂在2016年的“减员增效”中对部分人员实行分流,规定分流人员第一年可以到原单位领取工资的100%,从第二年起,以后每年只能在原单位按上一年的![]() 领取工资,该厂根据分流人员的技术特长,计划创办新的经济实体,该经济实体预计第一年属投资阶段,第二年每人可获得
领取工资,该厂根据分流人员的技术特长,计划创办新的经济实体,该经济实体预计第一年属投资阶段,第二年每人可获得![]() 元收入,从第三年起每人每年的收入可在上一年的基础上递增50%,如果某人分流后工资的收入每年
元收入,从第三年起每人每年的收入可在上一年的基础上递增50%,如果某人分流后工资的收入每年![]() 元,分流后进入新经济实体,第
元,分流后进入新经济实体,第![]() 年的收入为
年的收入为![]() 元;
元;
(1)求![]() 的通项公式;
的通项公式;
(2)当![]() 时,是否一定可以保证这个人分流一年后的收入永远超过分流前的年收入?
时,是否一定可以保证这个人分流一年后的收入永远超过分流前的年收入?
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数![]() .
.
(1)求函数![]() 的最小正周期;
的最小正周期;
(2)将函数![]() 的图象向右平移
的图象向右平移![]() 个单位长度,再向下平移
个单位长度,再向下平移![]() (
(![]() )个单位长度后得到函数
)个单位长度后得到函数![]() 的图象,且函数
的图象,且函数![]() 的最大值为2.
的最大值为2.
(ⅰ)求函数![]() 的解析式; (ⅱ)证明:存在无穷多个互不相同的正整数
的解析式; (ⅱ)证明:存在无穷多个互不相同的正整数![]() ,使得
,使得![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆![]() 的两个焦点分别为
的两个焦点分别为![]() ,短轴的两个端点分别为
,短轴的两个端点分别为![]() .
.
(Ⅰ)若![]() 为等边三角形,求椭圆
为等边三角形,求椭圆![]() 的方程;
的方程;
(Ⅱ)若椭圆![]() 的短轴长为
的短轴长为![]() ,过点
,过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 两点,且
两点,且![]() ,求直线
,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目: 来源: 题型:
【题目】为发挥体育咋核心素养时代的独特育人价值,越来越多的中学生已将某些体育项目纳入到学生的必修课程,某中学计划在高一年级开设游泳课程,为了解学生对游泳的兴趣,某数学研究学习小组随机从该校高一年级学生抽取了100人进行调查.
班 级 | 一(1) | 一(2) | 一(3) | 一(4) | 一(5) | 一(6) | 一(7) | 一(8) | 一(9) | 一(10) |
市级比赛 获奖人数 | 2 | 2 | 3 | 3 | 4 | 4 | 3 | 3 | 4 | 2 |
市级以上比 赛获奖人数 | 2 | 2 | 1 | 0 | 2 | 3 | 3 | 2 | 1 | 2 |
(1)已知在被抽取的女生中有6名高一(1)班学生,其中3名对游泳有兴趣,现在从这6名学生中最忌抽取3人,求至少有2人对游泳有兴趣的概率;
(2)该研究性学习小组在调查发现,对游泳有兴趣的学生中有部分曾在市级以上游泳比赛中获奖,如上表所示,若从高一(8)班和高一(9)班获奖学生中随机各抽取2人进行跟踪调查.记选中的4人中市级以上游泳比赛获奖的人数为![]() ,求随机变量
,求随机变量![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目: 来源: 题型:
【题目】在直角坐标系xOy中,直线l的参数方程为![]() (t为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为
(t为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为![]() ,直线l与曲线C交于不同的两点A,B.
,直线l与曲线C交于不同的两点A,B.
(1)求曲线C的参数方程;
(2)若点P为直线与x轴的交点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com