
科目: 来源: 题型:
【题目】在直角坐标系![]() 中,已知抛物线
中,已知抛物线![]()
![]() 上一点
上一点![]() 到焦点
到焦点![]() 的距离为6,点
的距离为6,点![]() 为其准线
为其准线![]() 上的任意一点,过点
上的任意一点,过点![]() 作抛物线
作抛物线![]() 的两条切线,切点分别为
的两条切线,切点分别为![]() .
.
(1)求抛物线![]() 的方程;
的方程;
(2)当点![]() 在
在![]() 轴上时,证明:
轴上时,证明:![]() 为等腰直角三角形.
为等腰直角三角形.
(3)证明:![]() 为直角三角形.
为直角三角形.
查看答案和解析>>
科目: 来源: 题型:
【题目】在四棱锥![]() 中,
中,![]() 平面
平面![]() ,
,![]() 是正三角形,
是正三角形,![]() ,
,![]() .
.

(1)求平面![]() 与平面
与平面![]() 所成的锐二面角的大小;
所成的锐二面角的大小;
(2)点![]() 为线段
为线段![]() 上的一动点,设异面直线
上的一动点,设异面直线![]() 与直线
与直线![]() 所成角的大小为
所成角的大小为![]() ,当
,当![]() 时,试确定点
时,试确定点![]() 的位置.
的位置.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知数列![]() ,若对任意的
,若对任意的![]() ,
,![]() ,
,![]() ,存在正数
,存在正数![]() 使得
使得![]() ,则称数列
,则称数列![]() 具有守恒性质,其中最小的
具有守恒性质,其中最小的![]() 称为数列
称为数列![]() 的守恒数,记为
的守恒数,记为![]() .
.
(1)若数列![]() 是等差数列且公差为
是等差数列且公差为![]()
![]() ,前
,前![]() 项和记为
项和记为![]() .
.
①证明:数列![]() 具有守恒性质,并求出其守恒数.
具有守恒性质,并求出其守恒数.
②数列![]() 是否具有守恒性质?并说明理由.
是否具有守恒性质?并说明理由.
(2)若首项为1且公比不为1的正项等比数列![]() 具有守恒性质,且
具有守恒性质,且![]() ,求公比
,求公比![]() 值的集合.
值的集合.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数![]() ,
,![]() ,
,![]() .
.
(1)若曲线![]() 在
在![]() 处的切线与曲线
处的切线与曲线![]() 相切,求
相切,求![]() 的值;
的值;
(2)当![]() 时,函数
时,函数![]() 的图象恒在函数
的图象恒在函数![]() 的图象的下方,求
的图象的下方,求![]() 的取值范围;
的取值范围;
(3)若函数![]() 恰有2个不相等的零点,求实数
恰有2个不相等的零点,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,某同学在素质教育基地通过自己设计、选料、制作,打磨出了一个作品,作品由三根木棒![]() ,
,![]() ,
,![]() 组成,三根木棒有相同的端点
组成,三根木棒有相同的端点![]() (粗细忽略不计),且
(粗细忽略不计),且![]() 四点在同一平面内,
四点在同一平面内,![]()
![]() ,
,![]() ,木棒
,木棒![]() 可绕点O任意旋转,设BC的中点为D.
可绕点O任意旋转,设BC的中点为D.
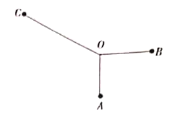
(1)当![]() 时,求OD的长;
时,求OD的长;
(2)当木棒OC绕点O任意旋转时,求AD的长的范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】在直角坐标系![]() 中,已知椭圆
中,已知椭圆![]() ,若圆
,若圆![]()
![]() 的一条切线与椭圆
的一条切线与椭圆![]() 有两个交点
有两个交点![]() ,且
,且![]() .
.
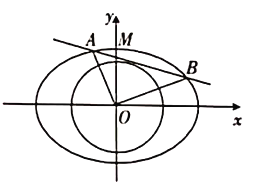
(1)求圆![]() 的方程;
的方程;
(2)已知椭圆![]() 的上顶点为
的上顶点为![]() ,点
,点![]() 在圆
在圆![]() 上,直线
上,直线![]() 与椭圆
与椭圆![]() 相交于另一点
相交于另一点![]() ,且
,且![]() ,求直线
,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目: 来源: 题型:
【题目】2022年北京冬奥会的申办成功与“3亿人上冰雪”口号的提出,将冰雪这个冷项目迅速炒“热”.北京某综合大学计划在一年级开设冰球课程,为了解学生对冰球运动的兴趣,随机从该校一年级学生中抽取了100人进行调查,其中女生中对冰球运动有兴趣的占![]() ,而男生有10人表示对冰球运动没有兴趣额.
,而男生有10人表示对冰球运动没有兴趣额.
(1)完成![]() 列联表,并回答能否有
列联表,并回答能否有![]() 的把握认为“对冰球是否有兴趣与性别有关”?
的把握认为“对冰球是否有兴趣与性别有关”?
有兴趣 | 没兴趣 | 合计 | |
男 | 55 | ||
女 | |||
合计 |
(2)已知在被调查的女生中有5名数学系的学生,其中3名对冰球有兴趣,现在从这5名学生中随机抽取3人,求至少有2人对冰球有兴趣的概率.
附表:
| 0.150 | 0.100 | 0.050 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,一张坐标纸上一已作出圆![]() 及点
及点![]() ,折叠此纸片,使
,折叠此纸片,使![]() 与圆周上某点
与圆周上某点![]() 重合,每次折叠都会留下折痕,设折痕与直线
重合,每次折叠都会留下折痕,设折痕与直线![]() 的交点为
的交点为![]() ,令点
,令点![]() 的轨迹为
的轨迹为![]() .
.

(1)求轨迹![]() 的方程;
的方程;
(2)若直线![]() 与轨迹
与轨迹![]() 交于两个不同的点
交于两个不同的点![]() ,且直线
,且直线![]() 与以
与以![]() 为直径的圆相切,若
为直径的圆相切,若![]() ,求
,求![]() 的面积的取值范围.
的面积的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在四棱锥![]() 中,平面
中,平面![]() 平面ABCD,底面ABCD是直角梯形,
平面ABCD,底面ABCD是直角梯形,![]() ,
,![]() ,
,![]() .
.
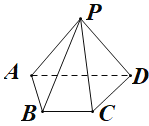
(1)在线段PA上找一点E,使得![]() 平面PCD,并证明;
平面PCD,并证明;
(2)在(1)的条件下,若![]() ,求点E到平面PCD的距离.
,求点E到平面PCD的距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com