
科目: 来源: 题型:
【题目】在直角坐标系xOy中,曲线C:x2=6y与直线l:y=kx+3交于M,N两点.
(1)设M,N到y轴的距离分别为d1,d2,证明:d1d2为定值.
(2)y轴上是否存在点P,使得当k变动时,总有∠OPM=∠OPN?若存在,求以线段OP为直径的圆的方程;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
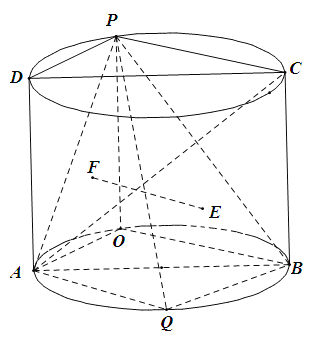
【题目】如图,圆柱的轴截面![]() 是边长为2的正方形,点
是边长为2的正方形,点![]() 是圆弧
是圆弧![]() 上的一动点(不与
上的一动点(不与![]() 重合),点
重合),点![]() 是圆弧
是圆弧![]() 的中点,且点
的中点,且点![]() 在平面
在平面![]() 的两侧.
的两侧.
(1)证明:平面![]() 平面
平面![]() ;
;
(2)设点![]() 在平面
在平面![]() 上的射影为点
上的射影为点![]() ,点
,点![]() 分别是
分别是![]() 和
和![]() 的重心,当三棱锥
的重心,当三棱锥![]() 体积最大时,回答下列问题.
体积最大时,回答下列问题.
(ⅰ)证明:![]() 平面
平面![]() ;
;
(ⅱ)求平面![]() 与平面
与平面![]() 所成二面角的正弦值.
所成二面角的正弦值.
查看答案和解析>>
科目: 来源: 题型:
【题目】某工厂生产的产品中分正品与次品,正品重![]() ,次品重
,次品重![]() ,现有5袋产品(每袋装有10个产品),已知其中有且只有一袋次品(10个产品均为次品)如果将5袋产品以1~5编号,第
,现有5袋产品(每袋装有10个产品),已知其中有且只有一袋次品(10个产品均为次品)如果将5袋产品以1~5编号,第![]() 袋取出
袋取出![]() 个产品(
个产品(![]() ),并将取出的产品一起用秤(可以称出物体重量的工具)称出其重量
),并将取出的产品一起用秤(可以称出物体重量的工具)称出其重量![]() ,若次品所在的袋子的编号是2,此时的重量
,若次品所在的袋子的编号是2,此时的重量![]() _________
_________![]() ;若次品所在的袋子的编号是
;若次品所在的袋子的编号是![]() ,此时的重量
,此时的重量![]() _______
_______![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() 是椭圆上一动点(与左、右顶点不重合)已知
是椭圆上一动点(与左、右顶点不重合)已知![]() 的内切圆半径的最大值为
的内切圆半径的最大值为![]() ,椭圆的离心率为
,椭圆的离心率为![]() .
.
(1)求椭圆C的方程;
(2)过![]() 的直线
的直线![]() 交椭圆
交椭圆![]() 于
于![]() 两点,过
两点,过![]() 作
作![]() 轴的垂线交椭圆
轴的垂线交椭圆![]() 与另一点
与另一点![]() (
(![]() 不与
不与![]() 重合).设
重合).设![]() 的外心为
的外心为![]() ,求证
,求证![]() 为定值.
为定值.
查看答案和解析>>
科目: 来源: 题型:
【题目】为实现有效利用扶贫资金,增加贫困村民的收入,扶贫工作组结合某贫困村水质优良的特点,决定利用扶贫资金从外地购买甲、乙、丙三种鱼苗在鱼塘中进行养殖试验,试验后选择其中一种进行大面积养殖,已知鱼苗甲的自然成活率为0.8.鱼苗乙,丙的自然成活率均为0.9,且甲、乙、丙三种鱼苗是否成活相互独立.
(1)试验时从甲、乙,丙三种鱼苗中各取一尾,记自然成活的尾数为![]() ,求
,求![]() 的分布列和数学期望;
的分布列和数学期望;
(2)试验后发现乙种鱼苗较好,扶贫工作组决定购买![]() 尾乙种鱼苗进行大面积养殖,为提高鱼苗的成活率,工作组采取增氧措施,该措施实施对能够自然成活的鱼苗不产生影响.使不能自然成活的鱼苗的成活率提高了50%.若每尾乙种鱼苗最终成活后可获利10元,不成活则亏损2元,且扶贫工作组的扶贫目标是获利不低于37.6万元,问需至少购买多少尾乙种鱼苗?
尾乙种鱼苗进行大面积养殖,为提高鱼苗的成活率,工作组采取增氧措施,该措施实施对能够自然成活的鱼苗不产生影响.使不能自然成活的鱼苗的成活率提高了50%.若每尾乙种鱼苗最终成活后可获利10元,不成活则亏损2元,且扶贫工作组的扶贫目标是获利不低于37.6万元,问需至少购买多少尾乙种鱼苗?
查看答案和解析>>
科目: 来源: 题型:
【题目】由我国引领的5G时代已经到来,5G的发展将直接带动包括运营、制造、服务在内的通信行业整体的快速发展,进而对![]() 增长产生直接贡献,并通过产业间的关联效应和波及效应,间接带动国民经济各行业的发展,创造岀更多的经济增加值.如图是某单位结合近年数据,对今后几年的5G经济产出所做的预测.结合下图,下列说法正确的是( )
增长产生直接贡献,并通过产业间的关联效应和波及效应,间接带动国民经济各行业的发展,创造岀更多的经济增加值.如图是某单位结合近年数据,对今后几年的5G经济产出所做的预测.结合下图,下列说法正确的是( )
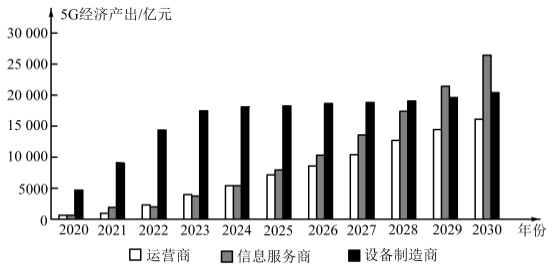
A.5G的发展带动今后几年的总经济产出逐年增加
B.设备制造商的经济产出前期增长较快,后期放缓
C.设备制造商在各年的总经济产出中一直处于领先地位
D.信息服务商与运营商的经济产出的差距有逐步拉大的趋势
查看答案和解析>>
科目: 来源: 题型:
【题目】定义:如果函数![]() 在定义域内给定区间
在定义域内给定区间![]() 上存在
上存在![]() ,满足
,满足![]() ,则称函数
,则称函数![]() 是
是![]() 上的“平均值函数”,
上的“平均值函数”,![]() 是它的一个均值点.例如y=| x |是
是它的一个均值点.例如y=| x |是![]() 上的“平均值函数”,0就是它的均值点.给出以下命题:
上的“平均值函数”,0就是它的均值点.给出以下命题:
①函数![]() 是
是![]() 上的“平均值函数”.
上的“平均值函数”.
②若![]() 是
是![]() 上的“平均值函数”,则它的均值点x0≥
上的“平均值函数”,则它的均值点x0≥![]() .
.
③若函数![]() 是
是![]() 上的“平均值函数”,则实数m的取值范围是
上的“平均值函数”,则实数m的取值范围是![]() .
.
④若![]() 是区间[a.,b] (b>a.≥1)上的“平均值函数”,
是区间[a.,b] (b>a.≥1)上的“平均值函数”,![]() 是它的一个均值点,则
是它的一个均值点,则![]() .
.
其中的真命题有_________.(写出所有真命题的序号)
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数f(x)=ex-ax-1(e为自然对数的底数),a>0.
(1)若函数f(x)恰有一个零点,证明:aa=ea-1;
(2)若f(x)≥0对任意x∈R恒成立,求实数a的取值集合.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com