
科目: 来源: 题型:
【题目】按照我国《机动车交通事故责任强制保险条例》规定,交强险是车主必须为机动车购买的险种,若普通7座以下私家车投保交强险第一年的费用(基准保费)统一为![]() 元,在下一年续保时,实行的是保费浮动机制,保费与上一、二、三个年度车辆发生道路交通事故的情况相关联,发生交通事故的次数越多,费率也就越高,具体浮动情況如表:
元,在下一年续保时,实行的是保费浮动机制,保费与上一、二、三个年度车辆发生道路交通事故的情况相关联,发生交通事故的次数越多,费率也就越高,具体浮动情況如表:

某机构为了研究某一品牌普通7座以下私家车的投保情况,随机抽取了80辆车龄已满三年的该品牌同型号私家车在下一年续保时的情况,统计得到了下面的表格:

以这80辆该品牌车的投保类型的频率代替一辆车投保类型的概率,完成下列问题:
(1)某家庭有一辆该品牌车且车龄刚满三年,记![]() 为该车在第四年续保时的费用,求
为该车在第四年续保时的费用,求![]() 的分布列;
的分布列;
(2)某销售商专门销售这一品牌的二手车,且将下一年的交强险保费高于基准保费的车辆记为事故车.
①若该销售商购进三辆车(车龄已满三年)该品牌二手车,求这三辆车中至少有2辆事故车的概率;
②假设购进一辆事故车亏损4000元,一辆非事故车盈利8000元.若该销售商一次购进100辆(车龄已满三年)该品牌二手车,求其获得利润的期望值.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知曲线![]() 上任意一点
上任意一点![]() 满足
满足![]() ,直线
,直线![]() 的方程为
的方程为![]() ,且与曲线
,且与曲线![]() 交于不同两点
交于不同两点![]() ,
,![]() .
.
(1)求曲线![]() 的方程;
的方程;
(2)设点![]() ,直线
,直线![]() 与
与![]() 的斜率分别为
的斜率分别为![]() ,
,![]() ,且
,且![]() ,判断直线
,判断直线![]() 是否过定点?若过定点,求该定点的坐标.
是否过定点?若过定点,求该定点的坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】某医科大学实习小组为研究实习地昼夜温差与患感冒人数之间的关系,分别到当地气象部门和某医院抄录了1月份至3月份每月5日、20日的昼夜温差情况与因患感冒而就诊的人数,得到如表资料:
日期 | 1月5日 | 1月20日 | 2月5日 | 2月20日 | 3月5日 | 3月20日 |
昼夜温差 | 10 | 11 | 13 | 12 | 8 | 6 |
就诊人数 | 22 | 25 | 29 | 26 | 16 | 12 |
该小组确定的研究方案是:先从这六组数据中随机选取4组数据求线性回归方程,再用剩余的2组数据进行检验.
(1)求剩余的2组数据都是20日的概率;
(2)若选取的是1月20日,2月5日,2月20日,3月5日四组数据.
①请根据这四组数据,求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() (
(![]() ,
,![]() 用分数表示);
用分数表示);
②若某日的昼夜温差为![]() ,预测当日就诊人数约为多少人?
,预测当日就诊人数约为多少人?
附参考公式: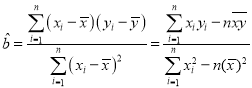 ,
,![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以平面直角坐标系
为参数),以平面直角坐标系![]() 的原点
的原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,椭圆
轴的正半轴为极轴建立极坐标系,椭圆![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的普通方程(写成一般式)和椭圆
的普通方程(写成一般式)和椭圆![]() 的直角坐标方程(写成标准方程);
的直角坐标方程(写成标准方程);
(2)若直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() ,
,![]() 两点,且与
两点,且与![]() 轴相交于点
轴相交于点![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】给出下列四个结论,其中正确的是( )
①从匀速传送的生产流水线上,每30分钟抽取一件产品进行检测,这样的抽样是分层抽样;②“![]() ”成立的必要而不充分条件是“
”成立的必要而不充分条件是“![]() ”;③若样本数据
”;③若样本数据![]() ,
,![]() ,…,
,…,![]() 的标准差为3,则
的标准差为3,则![]() ,
,![]() ,…,
,…,![]() 的方差为145;④
的方差为145;④![]() ,
,![]() ,
,![]() 是向量,则由“
是向量,则由“![]() ”类比得到“
”类比得到“![]() ”的结论是正确的.
”的结论是正确的.
A.①④B.②③C.①③D.②④
查看答案和解析>>
科目: 来源: 题型:
【题目】我国南北朝时期数学家、天文学家——祖暅,提出了著名的祖暅原理:“幂势既同,则积不容异也”.“幂”是截面积,“势”是几何体的高,意思是两等高几何体,若在每一等高处的两截面面积都相等,则两几何体体积相等.已知某不规则几何体与如图三视图所对应的几何体满足祖暅原理,则该不规则几何体的体积为( )
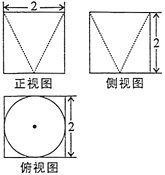
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数![]() .
.
(1)当![]() 时,若函数
时,若函数![]() 在
在![]() ,
,![]() (
(![]() )处导数相等,证明:
)处导数相等,证明:![]() ;
;
(2)是否存在![]() ,使直线
,使直线![]() 是曲线
是曲线![]() 的切线,也是曲线
的切线,也是曲线![]() 的切线,而且这样的直线
的切线,而且这样的直线![]() 是唯一的,如果存在,求出直线
是唯一的,如果存在,求出直线![]() 方程,如果不存在,请说明理由.
方程,如果不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】改革开放以来,我国农村7亿多贫困人口摆脱贫困,贫困发生率由1978年的97.5%下降到2018年底的1.4%,创造了人类减贫史上的中国奇迹,为全球减贫事业贡献了中国智慧和中国方案.“贫困发生率”是指低于贫困线的人口占全体人口的比例.2012年至2018年我国贫困发生率的数据如下表:
年份( | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 |
贫困发生率 | 10.2 | 8.5 | 7.2 | 5.7 | 4.5 | 3.1 | 1.4 |
(1)从表中所给的7个贫困发生率数据中任选两个,求至少有一个低于5%的概率;
(2)设年份代码![]() ,利用回归方程,分析2012年至2018年贫困发生率的变化情况,并预测2019年贫困发生率.
,利用回归方程,分析2012年至2018年贫困发生率的变化情况,并预测2019年贫困发生率.
附:回归直线![]() 的斜率和截距的最小二乘估计公式分别为:
的斜率和截距的最小二乘估计公式分别为: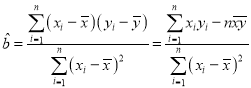 ,
,![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com