
科目: 来源: 题型:
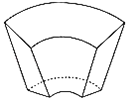
【题目】《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有曲池,上中周二丈,外周四丈,广一丈,下中周一丈四尺,外周二丈四尺,广五尺,深一丈,问积几何?”其意思为:“今有上下底面皆为扇形的水池,上底中周2丈,外周4丈,宽1丈;下底中周1丈4尺,外周长2丈4尺,宽5尺;深1丈.问它的容积是多少?”则该曲池的容积为( )立方尺(1丈=10尺,曲池:上下底面皆为扇形的土池,其容积公式为![]() [(2×上宽+下宽)
[(2×上宽+下宽)![]() (2×下宽+上宽)
(2×下宽+上宽)![]() ]×深)
]×深)
A.![]() B.1890C.
B.1890C.![]() D.
D.![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在多面体![]() 中,四边形
中,四边形![]() 为矩形,
为矩形,![]() ,
,![]() 均为等边三角形,
均为等边三角形,![]() ,
,![]() .
.
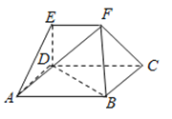
(Ⅰ)过![]() 作截面与线段
作截面与线段![]() 交于点
交于点![]() ,使得
,使得![]() 平面
平面![]() ,试确定点
,试确定点![]() 的位置,并予以证明;
的位置,并予以证明;
(Ⅱ)在(Ⅰ)的条件下,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知某民族品牌手机生产商为迎合市场需求,每年都会研发推出一款新型号手机.该公司现研发了一款新型智能手机并投入生产,生产这款手机的月固定成本为80万元,每生产1千台,须另投入27万元, 设该公司每月生产![]() 千台并能全部销售完,每1千台的销售收入为
千台并能全部销售完,每1千台的销售收入为![]() 万元,且
万元,且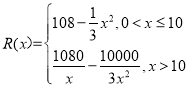 .为更好推广该产品,手机生产商每月还支付各类广告费用20万元.
.为更好推广该产品,手机生产商每月还支付各类广告费用20万元.
(Ⅰ)写出月利润![]() (万元)关于月产量
(万元)关于月产量![]() (千台)的函数解析式;
(千台)的函数解析式;
(Ⅱ)当月产量为多少千台时,该公司在这一型号的手机生产中所获月利润最大?
查看答案和解析>>
科目: 来源: 题型:
【题目】直线l的参数方程为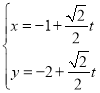 (t为参数),以坐标原点O为极点,x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为ρsin2θ=4acosθ,直线l与曲线C交于不同的两点M,N.
(t为参数),以坐标原点O为极点,x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为ρsin2θ=4acosθ,直线l与曲线C交于不同的两点M,N.
(1)求实数a的取值范围;
(2)已知a>0,设点P(﹣1,﹣2),若|PM|,|MN|,|PN|成等比数列,求a的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数![]() ,g(x)=b(x﹣1),其中a≠0,b≠0
,g(x)=b(x﹣1),其中a≠0,b≠0
(1)若a=b,讨论F(x)=f(x)﹣g(x)的单调区间;
(2)已知函数f(x)的曲线与函数g(x)的曲线有两个交点,设两个交点的横坐标分别为x1,x2,证明:![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】椭圆![]() (a>0,b>0)的左右焦点分别为F1,F2,与y轴正半轴交于点B,若△BF1F2为等腰直角三角形,且直线BF1被圆x2+y2=b2所截得的弦长为2,
(a>0,b>0)的左右焦点分别为F1,F2,与y轴正半轴交于点B,若△BF1F2为等腰直角三角形,且直线BF1被圆x2+y2=b2所截得的弦长为2,
(1)求椭圆的方程;
(2)直线l:y=kx+m与椭圆交于点A,C,线段AC的中点为M,射线MO与椭圆交于点P,点O为△PAC的重心,求证:△PAC的面积S为定值;
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在正三棱柱(底面为正三角形的直棱柱)ABC﹣A1B1C1中,已知AB=AA1=2,点Q为BC的中点.
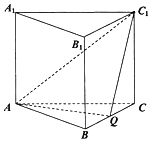
(1)求证:平面AQC1⊥平面B1BCC1;
(2)求直线CC1与平面AQC1所成角的正切值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com