
科目: 来源: 题型:
【题目】已知函数![]() .
.
(1)若关于![]() 的不等式
的不等式![]() 的解集为
的解集为![]() ,求函数
,求函数![]() 的最小值;
的最小值;
(2)是否存在实数![]() ,使得对任意
,使得对任意![]() ,存在
,存在![]() ,不等式
,不等式![]() 成立?若存在,求出
成立?若存在,求出![]() 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】一家小微企业生产某种小型产品的月固定成本为1万元,每生产1万件需要再投入2万元,假设该企业每个月可生产该小型产品![]() 万件并全部销售完,每万件的销售收入为
万件并全部销售完,每万件的销售收入为![]() 万元,且每生产1万件政府给予补助
万元,且每生产1万件政府给予补助![]() 万元.
万元.
(1)求该企业的月利润![]() (万元)关于月产量
(万元)关于月产量![]() (万件)的函数解析式;
(万件)的函数解析式;
(2)若月产量![]() 万件时,求企业在生产这种小型产品中所获得的月利润最大值(万元)及此时的月生产量值(万件).
万件时,求企业在生产这种小型产品中所获得的月利润最大值(万元)及此时的月生产量值(万件).
(注:月利润=月销售收入+月政府补助![]() 月总成本)
月总成本)
查看答案和解析>>
科目: 来源: 题型:
【题目】普通高中国家助学金,用于资助家庭困难的在校高中生.在本地,助学金分一等和二等两类,一等助学金每学期1250元,二等助学金每学期750元,并规定:属于农村建档立卡户的学生评一等助学金.某班有10名获得助学金的贫困学生,其中有3名属于农村建档立卡户,这10名学生中有4名获一等助学金,另6名获二等助学金.现从这10名学生中任选3名参加座谈会.
(Ⅰ)若事件A表示“选出的3名同学既有建档立卡户学生,又有非建档立卡户学生”,求A的概率;
(Ⅱ)设X为选出的3名同学一学期获助学金的总金额,求随机变量X的分布列和数学期望.
查看答案和解析>>
科目: 来源: 题型:
【题目】在直角坐标系xOy中,以坐标原点O为极点,以x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为ρ2﹣4ρsin(θ![]() )=0.
)=0.
(1)求曲线C的直角坐标方程;
(2)若直线l的参数方程是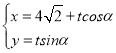 (α为参数),且α∈(
(α为参数),且α∈(![]() ,π)时,直线l与曲线C有且只有一个交点P,求点P的极径.
,π)时,直线l与曲线C有且只有一个交点P,求点P的极径.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图所示,该几何体是由一个直三棱柱ABE﹣DCF和一个四棱锥P﹣ABCD组合而成,其中EF=EA=EB=2,AE⊥EB,PA=PD![]() ,平面PAD∥平面EBCF.
,平面PAD∥平面EBCF.
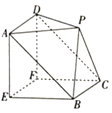
(1)证明:平面PBC∥平面AEFD;
(2)求直线AP与平面PCD所成角的正弦值.
查看答案和解析>>
科目: 来源: 题型:
【题目】某校从2011年到2018年参加“北约”,“华约”考试而获得加分的学生(每位学生只能参加“北约”,“华约”一种考试)人数可以通过以下表格反映出来.(为了方便计算,将2011年编号为1,2012年编号为2,依此类推……)
年份x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
人数y | 2 | 3 | 4 | 4 | 7 | 7 | 6 | 6 |
(1)据悉,该校2018年获得加分的6位同学中,有1位获得加20分,2位获得加15分,3位获得加10分,从该6位同学中任取两位,记该两位同学获得的加分之和为X,求X的分布列及期望.
(2)根据最近五年的数据,利用最小二乘法求出y与x之间的线性回归方程,并用以预测该校2019年参加“北约”,“华约”考试而获得加分的学生人数.(结果要求四舍五入至个位)
参考公式: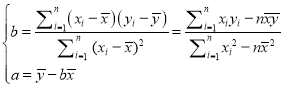
查看答案和解析>>
科目: 来源: 题型:
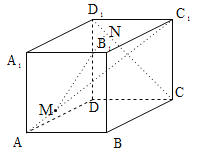
【题目】如图,直四棱柱ABCD﹣A1B1C1D1,底面ABCD是边长为6的正方形,M,N分别为线段AC1,D1C上的动点,若直线MN与平面B1BCC1没有公共点或有无数个公共点,点E为MN的中点,则E点的轨迹长度为_____.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知以线段EF为直径的圆内切于圆O:x2+y2=16.
(1)若点F的坐标为(﹣2,0),求点E的轨迹C的方程;
(2)在(1)的条件下,轨迹C上存在点T,使得![]() ,其中M,N为直线y=kx+b(b≠0)与轨迹C的交点,求△MNT的面积.
,其中M,N为直线y=kx+b(b≠0)与轨迹C的交点,求△MNT的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com