
科目: 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,左、右焦点分别是
,左、右焦点分别是![]() ,椭圆
,椭圆![]() 上短轴的一个端点与两个焦点构成的三角形的面积为
上短轴的一个端点与两个焦点构成的三角形的面积为![]() ;
;
(1)求椭圆![]() 的方程;
的方程;
(2)过![]() 作垂直于
作垂直于![]() 轴的直线
轴的直线![]() 交椭圆
交椭圆![]() 于
于![]() 两点(点
两点(点![]() 在第二象限),
在第二象限),![]() 是椭圆上位于直线
是椭圆上位于直线![]() 两侧的动点,若
两侧的动点,若![]() ,求证:直线
,求证:直线![]() 的斜率为定值.
的斜率为定值.
查看答案和解析>>
科目: 来源: 题型:
【题目】在直角坐标系![]() 中,倾斜角为
中,倾斜角为![]() 的直线
的直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).在以坐标原点为极点,
为参数).在以坐标原点为极点,![]() 轴正半轴为极轴的极坐标系中,曲线
轴正半轴为极轴的极坐标系中,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的普通方程与曲线
的普通方程与曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若直线![]() 与曲线
与曲线![]() 交于
交于![]() ,
,![]() 两点,且
两点,且![]() ,求直线
,求直线![]() 的倾斜角.
的倾斜角.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆![]() ,椭圆
,椭圆![]() 以
以![]() 的长轴为短轴,且两个椭圆的离心率相同,设O为坐标原点,点A、B分别在椭圆
的长轴为短轴,且两个椭圆的离心率相同,设O为坐标原点,点A、B分别在椭圆![]() 、
、![]() 上,若
上,若![]() ,则直线AB的斜率k为( ).
,则直线AB的斜率k为( ).
A.1B.-1C.![]() D.
D.![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】1852年,英国来华传教士伟烈亚力将《孙子算经》中“物不知数”问题的解法传至欧洲.1874年,英国数学家马西森指出此法符合1801年由高斯得到的关于同余式解法的一般性定理,因而西方称之为“中国剩余定理”.“中国剩余定理”讲的是一个关于整除的问题,例如求1到2000这2000个整数中,能被3除余1且被7除余1的数的个数,现由程序框图,其中MOD函数是一个求余函数,记![]() 表示m除以n的余数,例如
表示m除以n的余数,例如![]() ,则输出i为( ).
,则输出i为( ).
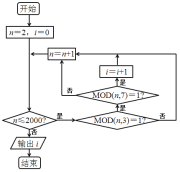
A.98B.97C.96D.95
查看答案和解析>>
科目: 来源: 题型:
【题目】在直角坐标系![]() 中,曲线C的参数方程为
中,曲线C的参数方程为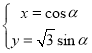 (
(![]() 为参数),直线
为参数),直线![]() 的斜率为1,在
的斜率为1,在![]() 轴上的截距为2
轴上的截距为2
(1)在直角坐标系![]() 中以O为极点,
中以O为极点,![]() 轴的正半轴为极轴建立极坐标系,点M的极坐标为
轴的正半轴为极轴建立极坐标系,点M的极坐标为![]() ,判断点M与直线
,判断点M与直线![]() 的位置关系;
的位置关系;
(2)设点A是曲线C上的任意点,求它到直线![]() 的距离的最大值
的距离的最大值
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆![]() 的右焦点为F
的右焦点为F![]() ,点B是椭圆C的短轴的一个端点,ΔOFB的面积为
,点B是椭圆C的短轴的一个端点,ΔOFB的面积为![]() ,椭圆C上的两点H、G关于原点O对称,且
,椭圆C上的两点H、G关于原点O对称,且![]() 、
、![]() 的等差中项为2
的等差中项为2
(1)求椭圆的方程;
(2)是否存在过点M(2,1)的直线![]() 与椭圆C交于不同的两点P、Q,且使得
与椭圆C交于不同的两点P、Q,且使得![]() 成立?若存在,试求出直线
成立?若存在,试求出直线![]() 的方程;若不存在,请说明理由
的方程;若不存在,请说明理由
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在等腰梯形ABCD中,AB//CD,∠ABC=![]() ,BC=CD=CE=1,EC⊥平面ABCD,EF
,BC=CD=CE=1,EC⊥平面ABCD,EF![]() AC,P是线段EF上的动点
AC,P是线段EF上的动点
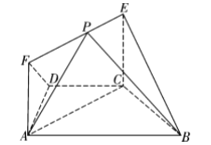
(1)求证:平面BCE⊥平面ACEF;
(2)求平面PAB与平面BCE所成锐二面角![]() 的最小值
的最小值
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com