
科目: 来源: 题型:
【题目】某城市为了解游客人数的变化规律,提高旅游服务质量,收集并整理了2017年1月至2019年12月期间月接待游客量(单位:万人)的数据,绘制了下面的折线图.根据该折线图,下列结论错误的是( )
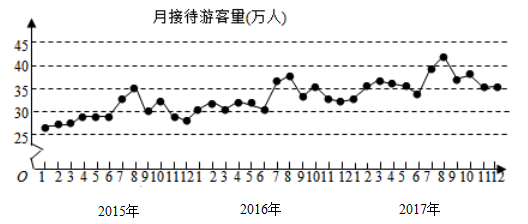
A.年接待游客量逐年增加
B.各年的月接待游客量高峰期大致在8月
C.2017年1月至12月月接待游客量的中位数为30万人
D.各年1月至6月的月接待游客量相对于7月至12月,波动性更小,变化比较平稳
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆![]() :
:![]() (
(![]() )的左、右焦点分别为
)的左、右焦点分别为![]() ,焦距为
,焦距为![]() ,过点
,过点![]() 作直线交椭圆
作直线交椭圆![]() 于
于![]() 两点,
两点,![]() 的周长为
的周长为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)若斜率为![]() 的直线
的直线![]() 与椭圆相交于
与椭圆相交于![]() 两点,求定点
两点,求定点![]() 与交点
与交点![]() 所构成的三角形
所构成的三角形![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目: 来源: 题型:
【题目】陆良县2017届和2018届都取得了辉煌的成绩,两年均有人考入清华大学或北京大学,600分以上的考生进一步创历史新高.对此北辰中学某学习兴趣小组对2019届20名学生的数学成绩进行了调查,所得分数分组为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,据此制作的频率分布直方图如图所示.
,据此制作的频率分布直方图如图所示.

(1)求出直方图中的![]() 值;
值;
(2)利用直方图估计2019届20名学生分数的众数和中位数(同一组中的数据用该组区间的中点值作代表);
(3)若从分数在![]() 的学生中,随机的抽取2名学生进行辅导,求抽到的学生来自同一组的概率.
的学生中,随机的抽取2名学生进行辅导,求抽到的学生来自同一组的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】为了研究55岁左右的中国人睡眠质量与心脑血管病是否有关联,某机构在适龄人群中随机抽取了100万个样本,调查了他们每周是否至少三个晚上出现了三种失眠症状,![]() 症状:入睡困难;
症状:入睡困难;![]() 症状:醒得太早;
症状:醒得太早;![]() 症状:不能深度入睡或做梦,得到的调查数据如下:
症状:不能深度入睡或做梦,得到的调查数据如下:
数据1:出现![]() 症状人数为8.5万,出现
症状人数为8.5万,出现![]() 症状人数为9.3万,出现
症状人数为9.3万,出现![]() 症状人数为6.5万,其中含
症状人数为6.5万,其中含![]() 症状同时出现1.8万人,
症状同时出现1.8万人,![]() 症状同时出现1万人,
症状同时出现1万人,![]() 症状同时出现2万人,
症状同时出现2万人,![]() 症状同时出现0.5万人;
症状同时出现0.5万人;
数据2:同时有失眠症状和患心脑血管病的人数为5万人,没有失眠症状且无心脑血管病的人数为73万人.
(Ⅰ)依据上述数据试分析55岁左右的中国人患有失眠症的比例大约多少?
(Ⅱ)根据以上数据完成如下列联表,并根据所填列联表判断能否有95%的把握说明失眠与心脑血管病存在“强关联”?
失眠 | 不失眠 | 合计 | |
患心脑血管疾病 | |||
不患心脑血管疾病 | |||
合计 |
参考数据如下:
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 |
| 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
参考公式: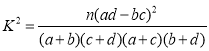
查看答案和解析>>
科目: 来源: 题型:
【题目】近年来,新能源汽车技术不断推陈出新,新产品不断涌现,在汽车市场上影响力不断增大.动力蓄电池技术作为新能源汽车的核心技术,它的不断成熟也是推动新能源汽车发展的主要动力.假定现在市售的某款新能源汽车上,车载动力蓄电池充放电循环次数达到2000次的概率为85%,充放电循环次数达到2500次的概率为35%.若某用户的自用新能源汽车已经经过了2000次充电,那么他的车能够充电2500次的概率为______.
查看答案和解析>>
科目: 来源: 题型:
【题目】大约在20世纪30年代,世界上许多国家都流传着这样一个题目:任取一个正整数![]() ,如果它是偶数,则除以2;如果它是奇数,则将它乘以3加1,这样反复运算,最后结果必然是1.这个题目在东方被称为“角谷猜想”,世界一流的大数学家都被其卷入其中,用尽了各种方法,甚至动用了最先进的电子计算机,验算到对700亿以内的自然数上述结论均为正确的,但却给不出一般性的证明.例如取
,如果它是偶数,则除以2;如果它是奇数,则将它乘以3加1,这样反复运算,最后结果必然是1.这个题目在东方被称为“角谷猜想”,世界一流的大数学家都被其卷入其中,用尽了各种方法,甚至动用了最先进的电子计算机,验算到对700亿以内的自然数上述结论均为正确的,但却给不出一般性的证明.例如取![]() ,则要想算出结果1,共需要经过的运算步数是( )
,则要想算出结果1,共需要经过的运算步数是( )
A.9B.10C.11D.12
查看答案和解析>>
科目: 来源: 题型:
【题目】工厂质检员从生产线上每半个小时抽取一件产品并对其某个质量指标![]() 进行检测,一共抽取了
进行检测,一共抽取了![]() 件产品,并得到如下统计表.该厂生产的产品在一年内所需的维护次数与指标
件产品,并得到如下统计表.该厂生产的产品在一年内所需的维护次数与指标![]() 有关,具体见下表.
有关,具体见下表.
质量指标 |
|
|
|
频数 |
|
|
|
一年内所需维护次数 |
|
|
|
(1)以每个区间的中点值作为每组指标的代表,用上述样本数据估计该厂产品的质量指标![]() 的平均值(保留两位小数);
的平均值(保留两位小数);
(2)用分层抽样的方法从上述样本中先抽取![]() 件产品,再从
件产品,再从![]() 件产品中随机抽取
件产品中随机抽取![]() 件产品,求这
件产品,求这![]() 件产品的指标
件产品的指标![]() 都在
都在内的概率;
(3)已知该厂产品的维护费用为![]() 元/次,工厂现推出一项服务:若消费者在购买该厂产品时每件多加
元/次,工厂现推出一项服务:若消费者在购买该厂产品时每件多加![]() 元,该产品即可一年内免费维护一次.将每件产品的购买支出和一年的维护支出之和称为消费费用.假设这
元,该产品即可一年内免费维护一次.将每件产品的购买支出和一年的维护支出之和称为消费费用.假设这![]() 件产品每件都购买该服务,或者每件都不购买该服务,就这两种情况分别计算每件产品的平均消费费用,并以此为决策依据,判断消费者在购买每件产品时是否值得购买这项维护服务?
件产品每件都购买该服务,或者每件都不购买该服务,就这两种情况分别计算每件产品的平均消费费用,并以此为决策依据,判断消费者在购买每件产品时是否值得购买这项维护服务?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com