
科目: 来源: 题型:
【题目】点![]() 与定点
与定点![]() 的距离和它到直线
的距离和它到直线![]() 的距离的比是常数
的距离的比是常数![]() ,设点
,设点![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求曲线![]() 的方程;
的方程;
(2)过点![]() 的直线
的直线![]() 与曲线
与曲线![]() 交于
交于![]() ,
,![]() 两点,设
两点,设![]() 的中点为
的中点为![]() ,
,![]() ,
,![]() 两点为曲线
两点为曲线![]() 上关于原点
上关于原点![]() 对称的两点,且
对称的两点,且![]() (
(![]() ),求四边形
),求四边形![]() 面积的取值范围.
面积的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】在统计调查中,问卷的设计是一门很大的学问,特别是对一些敏感性问题.例如学生在考试中有无作弊现象,社会上的偷税漏税等.更要精心设计问卷.设法消除被调查者的顾虑,使他们能够如实回答问题,否则被调查者往往会拒绝冋答,或不提供真实情况,为了调查中学生中的早恋现象,随机抽出300名学生,调查中使用了两个问題.①你的学籍号的最后一位数是奇数(学籍号的后四位是序号);②你是否有早恋现象,让被调查者从装有4个红球,6个黑球(除颜色外完全相同)的袋子中随机摸取两个球.摸到两球同色的学生如实回答第一个问题,摸到两球异色的学生如实回答第二个问题,回答“是”的人往一个盒子中放一个小石子,回答“否”的人什么都不放,后来在盒子中收到了78个小石子.
(1)你能否估算出中学生早恋人数的百分比?
(2)若从该地区中学生中随机抽取一个班(40人),设其中恰有![]() 个人存在早恋的现象,求
个人存在早恋的现象,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目: 来源: 题型:
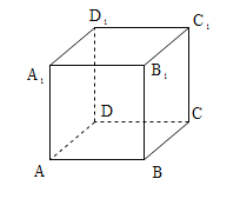
【题目】如图,正方体![]() 的棱长为1,有下列四个命题:
的棱长为1,有下列四个命题:
①![]() 与平面
与平面![]() 所成角为
所成角为![]() ;
;
②三棱锥![]() 与三棱锥
与三棱锥![]() 的体积比为
的体积比为![]() ;
;
③过点![]() 作平面
作平面![]() ,使得棱
,使得棱![]() ,
,![]() ,
,![]() 在平面
在平面![]() 上的正投影的长度相等,则这样的平面
上的正投影的长度相等,则这样的平面![]() 有且仅有一个;
有且仅有一个;
④过![]() 作正方体的截面,设截面面积为
作正方体的截面,设截面面积为![]() ,则
,则![]() 的最小值为
的最小值为![]() .
.
上述四个命题中,正确命題的序号为______.
查看答案和解析>>
科目: 来源: 题型:
【题目】造纸术是我国古代四大发明之一.纸张的规格是指纸张制成后,经过修整切边,裁成一定的尺寸.现在我国采用国际标准,规定以![]() 、
、![]() 、…、
、…、![]() ;
;![]() 、
、![]() 、…、
、…、![]() 等标记来表示纸张的幅面规格.复印纸幅面规格只采用
等标记来表示纸张的幅面规格.复印纸幅面规格只采用![]() 系列和
系列和![]() 系列,其中
系列,其中![]() 系列的幅面规格为:①
系列的幅面规格为:①![]() 规格的纸张的幅宽(以
规格的纸张的幅宽(以![]() 表示)和长度(以
表示)和长度(以![]() 表示)的比例关系为
表示)的比例关系为![]() ;②将
;②将![]() 纸张沿长度方向对开成两等分,便成为
纸张沿长度方向对开成两等分,便成为![]() 规格.
规格.![]() 纸张沿长度方向对开成两等分,便成为
纸张沿长度方向对开成两等分,便成为![]() 规格,…,如此对开至
规格,…,如此对开至![]() 规格.现有
规格.现有![]() 、
、![]() 、
、![]() 、…、
、…、![]() 纸各一张.若
纸各一张.若![]() 纸的面积为
纸的面积为![]() ,则这9张纸的面积之和等于______
,则这9张纸的面积之和等于______![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】天文学中为了衡量星星的明暗程度,古希腊天文学家喜帕恰斯(![]() ,又名依巴谷)在公元前二世纪首先提出了星等这个概念.星等的数值越小,星星就越亮;星等的数值越大,它的光就越暗.到了1850年,由于光度计在天体光度测量中的应用,英国天文学家普森(
,又名依巴谷)在公元前二世纪首先提出了星等这个概念.星等的数值越小,星星就越亮;星等的数值越大,它的光就越暗.到了1850年,由于光度计在天体光度测量中的应用,英国天文学家普森(![]() )又提出了衡量天体明暗程度的亮度的概念.天体的明暗程度可以用星等或亮度来描述.两颗星的星等与亮度满足
)又提出了衡量天体明暗程度的亮度的概念.天体的明暗程度可以用星等或亮度来描述.两颗星的星等与亮度满足![]() .其中星等为
.其中星等为![]() 的星的亮度为
的星的亮度为![]() .已知“心宿二”的星等是1.00.“天津四” 的星等是1.25.“心宿二”的亮度是“天津四”的
.已知“心宿二”的星等是1.00.“天津四” 的星等是1.25.“心宿二”的亮度是“天津四”的![]() 倍,则与
倍,则与![]() 最接近的是(当
最接近的是(当![]() 较小时,
较小时, ![]() )
)
A.1.24B.1.25C.1.26D.1.27
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆![]() :
:![]() (
(![]() )的左焦点为
)的左焦点为![]() ,其中四个顶点围成的四边形面积为
,其中四个顶点围成的四边形面积为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)过点![]() 的直线
的直线![]() 与曲线
与曲线![]() 交于
交于![]() ,
,![]() 两点,设
两点,设![]() 的中点为
的中点为![]() ,
,![]() ,
,![]() 两点为椭圆
两点为椭圆![]() 上关于原点
上关于原点![]() 对称的两点,且
对称的两点,且![]() (
(![]() ),求四边形
),求四边形![]() 面积的最小值.
面积的最小值.
查看答案和解析>>
科目: 来源: 题型:
【题目】在统计调查中,问卷的设计是一门很大的学问,特别是对一些敏感性问题.例如学生在考试中有无作弊现象,社会上的偷税漏税等,更要精心设计问卷.设法消除被调查者的顾虑,使他们能够如实回答问题,否则被调查者往往会拒绝回答,或不提供真实情况.为了调查中学生中的早恋现象,随机抽出200名学生,调查中使用了两个问题.①你的血型是A型或B型(资料:我国人口![]() 型血比例41%,
型血比例41%,![]() 型血比例28%,
型血比例28%,![]() 型血比例24%.
型血比例24%.![]() 型血比例7% ).②你是否有早恋现象,让被调查者掷两枚骰子,点数之和为奇数的学生如实回答第一个问题.点数之和为偶数的学生如实回答第二个问题,回答“是”的人往一个盒子中放一个小石子,回答“否”的人什么都不放,后来在盒子中收到了57个小石子.
型血比例7% ).②你是否有早恋现象,让被调查者掷两枚骰子,点数之和为奇数的学生如实回答第一个问题.点数之和为偶数的学生如实回答第二个问题,回答“是”的人往一个盒子中放一个小石子,回答“否”的人什么都不放,后来在盒子中收到了57个小石子.
(1)试计算掷两枚骰子点数之和为偶数的机率;
(2)你能否估算出中学生早恋人数的百分比?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com