
科目: 来源: 题型:
【题目】在数列{an}中,a1=3,且对任意的正整数n,都有an+1=λan+2×3n,其中常数λ>0.
(1)设bn![]() .当λ=3时,求数列{bn}的通项公式;
.当λ=3时,求数列{bn}的通项公式;
(2)若λ≠1且λ≠3,设cn=an![]() ,证明:数列{cn}为等比数列;
,证明:数列{cn}为等比数列;
(3)当λ=4时,对任意的n∈N*,都有an≥M,求实数M的最大值.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,已知椭圆![]() 的离心率为
的离心率为![]() ,右焦点F到右准线的距离为3.
,右焦点F到右准线的距离为3.
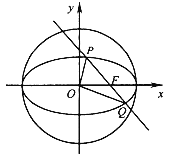
(1)求椭圆C的标准方程;
(2)设过F的直线l与椭圆C相交于P,Q两点.已知l被圆O:x2+y2=a2截得的弦长为![]() ,求△OPQ的面积.
,求△OPQ的面积.
查看答案和解析>>
科目: 来源: 题型:
【题目】在四棱锥P﹣ABCD中,底面ABCD为平行四边形,PD⊥平面ABCD,BD=CD,E,F分别为BC,PD的中点.

(1)求证:EF∥平面PAB;
(2)求证:平面PBC⊥平面EFD.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,![]() ,
,![]() 是某景区的两条道路(宽度忽略不计,
是某景区的两条道路(宽度忽略不计,![]() 为东西方向),Q为景区内一景点,A为道路
为东西方向),Q为景区内一景点,A为道路![]() 上一游客休息区,已知
上一游客休息区,已知![]() ,
,![]() (百米),Q到直线
(百米),Q到直线![]() ,
,![]() 的距离分别为3(百米),
的距离分别为3(百米),![]() (百米),现新修一条自A经过Q的有轨观光直路并延伸至道路
(百米),现新修一条自A经过Q的有轨观光直路并延伸至道路![]() 于点B,并在B处修建一游客休息区.
于点B,并在B处修建一游客休息区.
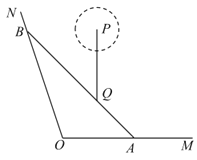
(1)求有轨观光直路![]() 的长;
的长;
(2)已知在景点Q的正北方6百米的P处有一大型组合音乐喷泉,喷泉表演一次的时长为9分钟,表演时,喷泉喷洒区域以P为圆心,r为半径变化,且t分钟时,![]() (百米)(
(百米)(![]() ,
,![]() ).当喷泉表演开始时,一观光车S(大小忽略不计)正从休息区B沿(1)中的轨道
).当喷泉表演开始时,一观光车S(大小忽略不计)正从休息区B沿(1)中的轨道![]() 以
以![]() (百米/分钟)的速度开往休息区A,问:观光车在行驶途中是否会被喷泉喷洒到,并说明理由.
(百米/分钟)的速度开往休息区A,问:观光车在行驶途中是否会被喷泉喷洒到,并说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数g(x)=ex﹣ax2﹣ax,h(x)=ex﹣2x﹣lnx.其中e为自然对数的底数.
(1)若f(x)=h(x)﹣g(x).
①讨论f(x)的单调性;
②若函数f(x)有两个不同的零点,求实数a的取值范围.
(2)已知a>0,函数g(x)恰有两个不同的极值点x1,x2,证明:![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系![]() 中,以坐标原点
中,以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,曲线
,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() ).
).
(1)写出曲线![]() 的直角坐标方程与曲线
的直角坐标方程与曲线![]() 的普通方程;
的普通方程;
(2)若射线![]() (
(![]() )与曲线
)与曲线![]() ,
,![]() 分别交于
分别交于![]() ,
,![]() 两点(不是原点),求
两点(不是原点),求![]() 的最大值.
的最大值.
查看答案和解析>>
科目: 来源: 题型:
【题目】我市为迎接一项重要的体育赛事,要完成![]() ,
,![]() 两座场馆的地基建造工程.某工程队需要把600名工人分成两组,一组完成
两座场馆的地基建造工程.某工程队需要把600名工人分成两组,一组完成![]() 场馆的甲级标准地基2000
场馆的甲级标准地基2000![]() ,同时另一组完成
,同时另一组完成![]() 场馆的乙级标准地基3000
场馆的乙级标准地基3000![]() ;据测算,完成甲级标准地基每平方米的工程量为50人
;据测算,完成甲级标准地基每平方米的工程量为50人![]() 天,完成乙级标准地基每平方米的工程量为30人
天,完成乙级标准地基每平方米的工程量为30人![]() 天.
天.
(1)若工程队分配![]() 名工人去
名工人去![]() 场馆,求
场馆,求![]() 场馆地基和
场馆地基和![]() 场馆地基建造时间
场馆地基建造时间![]() 和
和![]() (单位:天)的函数解析式;
(单位:天)的函数解析式;
(2)![]() 、
、![]() 两个场馆同时开工,该工程队如何分配两个场馆的工人数量,可以使得工期最短.
两个场馆同时开工,该工程队如何分配两个场馆的工人数量,可以使得工期最短.
(参考数据:![]() ,
,![]() ,
,![]() .备注:若地基面积为
.备注:若地基面积为![]() 平方米,每平方米的工程量为
平方米,每平方米的工程量为![]() 人/天,工人数
人/天,工人数![]() 人,则工期为
人,则工期为![]() 天.)
天.)
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数![]() (其中
(其中![]() 为常数,
为常数,![]() 为自然对数的底数,)
为自然对数的底数,)
(1)若对任意![]() ,不等式
,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值集合,
的取值集合,
(2)已知正数![]() 满足:存在
满足:存在![]() ,使不等式
,使不等式![]() 成立.
成立.
①求![]() 的取值集合;
的取值集合;
②试比较![]() 与
与![]() 的大小,并证明你的结论.
的大小,并证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com