
科目: 来源: 题型:
【题目】如图抛物线![]() 的焦点为
的焦点为![]() ,
,![]() 为抛物线上一点(
为抛物线上一点(![]() 在
在![]() 轴上方),
轴上方),![]() ,
,![]() 点到
点到![]() 轴的距离为4.
轴的距离为4.
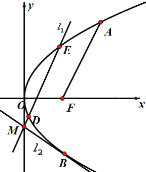
(1)求抛物线方程及点![]() 的坐标;
的坐标;
(2)是否存在![]() 轴上的一个点
轴上的一个点![]() ,过点
,过点![]() 有两条直线
有两条直线![]() ,满足
,满足![]() ,
,![]() 交抛物线
交抛物线![]() 于
于![]() 两点.
两点.![]() 与抛物线相切于点
与抛物线相切于点![]() (
(![]() 不为坐标原点),有
不为坐标原点),有![]() 成立,若存在,求出点
成立,若存在,求出点![]() 的坐标.若不存在,请说明理由.
的坐标.若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】甲、乙、丙、丁四个人到![]() ,
,![]() ,
,![]() 三个景点旅游,每个人只去一个景点,每个景点至少有一个人去,则甲不到
三个景点旅游,每个人只去一个景点,每个景点至少有一个人去,则甲不到![]() 景点的方案有( )
景点的方案有( )
A.18种B.12种C.36种D.24种
查看答案和解析>>
科目: 来源: 题型:
【题目】设数列{an}的前n项和为Sn,已知ban-2n=(b-1)Sn.
(1)证明:当b=2时,{an-n·2n-1}是等比数列;
(2)求{an}的通项公式.
查看答案和解析>>
科目: 来源: 题型:
【题目】某车间生产甲、乙两种产品,已知制造一件甲产品需要![]() 种元件5个,
种元件5个,![]() 种元件2个,制造一件乙种产品需要
种元件2个,制造一件乙种产品需要![]() 种元件3个,
种元件3个,![]() 种元件3个,现在只有
种元件3个,现在只有![]() 种元件180个,
种元件180个,![]() 种元件135个,每件甲产品可获利润20元,每件乙产品可获利润15元,试问在这种条件下,应如何安排生产计划才能得到最大利润?
种元件135个,每件甲产品可获利润20元,每件乙产品可获利润15元,试问在这种条件下,应如何安排生产计划才能得到最大利润?
查看答案和解析>>
科目: 来源: 题型:
【题目】某人准备投资1200万元办一所中学,为了考虑社会效益和经济效益,对该地区教育市场进行调查,得出一组数据,列表如下(以班级为单位).
市场调查表:
班级学生数 | 配备教师数 | 硬件建设费(万元) | 教师年薪(万元) | |
初中 | 50 | 2.0 | 28 | 1.2 |
高中 | 40 | 2.5 | 58 | 1.6 |
根据物价部门的有关规定:初中是义务教育阶段,收费标准适当控制,预计除书本费、办公费外,初中每人每年可收取600元.高中每人每年可收取1500元.因生源和环境等条件限制,办学规模以20至30个班为宜(含20个班与30个),教师实行聘任制.初、高中教育周期均为三年,设初中编制为![]() 个班,高中编制为
个班,高中编制为![]() 个班,请你合理地安排招生计划,使年利润最大.
个班,请你合理地安排招生计划,使年利润最大.
查看答案和解析>>
科目: 来源: 题型:
【题目】极坐标与参数方程
在直角坐标系![]() ,直线
,直线![]() 的参数方程是
的参数方程是![]() (
(![]() 为参数).在以
为参数).在以![]() 为极点,
为极点, ![]() 轴正半轴为极轴建立极坐标系中,曲线
轴正半轴为极轴建立极坐标系中,曲线![]() :
: ![]() .
.
(1)当![]() ,
, ![]() 时,判断直线
时,判断直线![]() 与曲线
与曲线![]() 的位置关系;
的位置关系;
(2)当![]() 时,若直线与曲
时,若直线与曲![]() 线
线![]() 相交于
相交于![]() ,
, ![]() 两点,设
两点,设![]() ,且
,且![]() ,求直线
,求直线![]() 的倾斜角.
的倾斜角.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com