
科目: 来源: 题型:
【题目】如图,已知![]() 是椭圆
是椭圆![]() 的左、右焦点,椭圆的短轴长为
的左、右焦点,椭圆的短轴长为![]() ,点
,点![]() 是椭圆
是椭圆![]() 上的一点,过点
上的一点,过点![]() 作
作![]() 轴的垂线交椭圆于另一点
轴的垂线交椭圆于另一点![]() (
(![]() 不过点
不过点![]() ),且
),且![]() 的周长的最大值为8.
的周长的最大值为8.
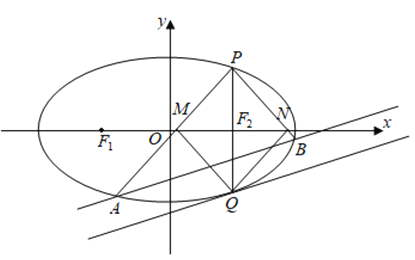
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若![]() 过焦点
过焦点![]() ,在椭圆上取两点
,在椭圆上取两点![]() ,连接
,连接![]() ,与
,与![]() 轴的交点分别为
轴的交点分别为![]() ,过点
,过点![]() 作椭圆的切线
作椭圆的切线![]() ,当四边形
,当四边形![]() 为菱形时,证明:直线
为菱形时,证明:直线![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】某工厂过去在生产过程中将污水直接排放到河流中对沿河环境造成了一定的污染,根据环保部门对该厂过去10年的监测数据,统计出了其每年污水排放量![]() (单位:吨)的频率分布表:
(单位:吨)的频率分布表:
污水排放量 |
|
|
|
|
频率 | 0.1 | 0.3 | 0.4 | 0.2 |
将污水排放量落入各组的频率作为概率,并假设每年该厂污水排放量相互独立.
(1)若不加以治理,根据上表中的数据,计算未来3年中至少有2年污水排放量不小于200吨的概率;
(2)根据环保部门的评估,该厂当年污水排放量![]() 时,对沿河环境及经济造成的损失为5万元;当年污水排放量
时,对沿河环境及经济造成的损失为5万元;当年污水排放量![]() 时,对沿河环境及经济造成的损失为10万元;当年污水排放量
时,对沿河环境及经济造成的损失为10万元;当年污水排放量![]() 时,对沿河环境及经济造成的损失为20万元;当年污水排放量
时,对沿河环境及经济造成的损失为20万元;当年污水排放量![]() 时,对沿河环境及经济造成的损失为50万元.为了保护环境,减少损失,该厂现有两种应对方案:
时,对沿河环境及经济造成的损失为50万元.为了保护环境,减少损失,该厂现有两种应对方案:
方案1:若该厂不采取治污措施,则需全部赔偿对沿河环境及经济造成的损失;
方案2:若该厂采购治污设备对所有产生的污水净化达标后再排放,则不需赔偿,采购设备的费用为10万元,每年设备维护等费用为15万元,该设备使用10年需重新更换.在接下来的10年里,试比较上述2种方案哪种能为该厂节约资金,并说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知定义在![]() 上的函数
上的函数![]() 满足
满足![]() ,且
,且![]() ,则下列说法正确的有( )
,则下列说法正确的有( )
(1)若函数![]() ,则函数
,则函数![]() 是奇函数;
是奇函数;
(2)![]() ;
;
(3)设函数![]() ,则函数
,则函数![]() 的图象经过点
的图象经过点![]() ;
;
(4)设![]() ,若数列
,若数列![]() 是等比数列,则
是等比数列,则![]() .
.
A.(2)(3)(4)B.(1)(3)(4)C.(1)(3)D.(1)(2)(3)(4)
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线l的参数方程为
中,直线l的参数方程为![]() (t为参数),以坐标原点O为极点,x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为
(t为参数),以坐标原点O为极点,x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为![]()
(1)求直线l的普通方程和曲线C的直角坐标方程;
(2)若直线l与曲线C相交于A,B两点.求![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】为提高产品质量,某企业质量管理部门经常不定期地对产品进行抽查检测,现对某条生产线上随机抽取的100个产品进行相关数据的对比,并对每个产品进行综合评分(满分100分),将每个产品所得的综合评分制成如图所示的频率分布直方图.记综合评分为80分及以上的产品为一等品.
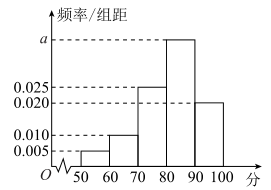
(1)求图中![]() 的值,并求综合评分的中位数;
的值,并求综合评分的中位数;
(2)用样本估计总体,视频率作为概率,在该条生产线中随机抽取3个产品,求所抽取的产品中一等品数的分布列和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com