
科目: 来源: 题型:
【题目】已知双曲线![]() 的右焦点到渐近线的距离为3.现有如下条件:①双曲线
的右焦点到渐近线的距离为3.现有如下条件:①双曲线![]() 的离心率为
的离心率为![]() ; ②双曲线
; ②双曲线![]() 与椭圆
与椭圆![]() 共焦点; ③双曲线右支上的一点
共焦点; ③双曲线右支上的一点![]() 到
到![]() 的距离之差是虚轴长的
的距离之差是虚轴长的![]() 倍.
倍.
请从上述3个条件中任选一个,得到双曲线![]() 的方程为_____________.
的方程为_____________.
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系![]() 中曲线
中曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以
为参数),以![]() 为极点,
为极点,![]() 轴的正半轴为极轴,建立极坐标系,直线
轴的正半轴为极轴,建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的普通方程以及直线
的普通方程以及直线![]() 的直角坐标方程;
的直角坐标方程;
(2)将曲线![]() 向左平移2个单位,再将曲线
向左平移2个单位,再将曲线![]() 上的所有点的横坐标缩短为原来的
上的所有点的横坐标缩短为原来的![]() ,得到曲线
,得到曲线![]() ,求曲线
,求曲线![]() 上的点到直线
上的点到直线![]() 的距离的最小值.
的距离的最小值.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,点
,点![]() 是椭圆
是椭圆![]() 上的点.
上的点.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)已知斜率存在又不经过原点的直线![]() 与圆
与圆![]() 相切,且与椭圆
相切,且与椭圆![]() 交于
交于![]() 两点.探究:在椭圆
两点.探究:在椭圆![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() ,若存在,请求出实数
,若存在,请求出实数![]() 的取值范围,若不存在,请说明理由.
的取值范围,若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】某大学棋艺协会定期举办“以棋会友”的竞赛活动,分别包括“中国象棋”、“围棋”、“五子棋”、“国际象棋”四种比赛,每位协会会员必须参加其中的两种棋类比赛,且各队员之间参加比赛相互独立;已知甲同学必选“中国象棋”,不选“国际象棋”,乙、丙两位同学从四种比赛中任选两种参与.
(1)求甲、乙同时参加围棋比赛的概率;
(2)记甲、乙、丙三人中选择“中国象棋”比赛的人数为![]() ,求
,求![]() 的分布列及期望.
的分布列及期望.
查看答案和解析>>
科目: 来源: 题型:
【题目】杨辉,字谦光,南宋时期杭州人.在他1261年所著的《详解九章算法》一书中,辑录了如图所示的三角形数表,称之为“开方作法本源”图,并说明此表引自11世纪中叶(约公元1050年)贾宪的《释锁算术》,并绘画了“古法七乘方图”.故此,杨辉三角又被称为“贾宪三角”.杨辉三角是一个由数字排列成的三角形数表,一般形式如下:
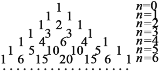
基于上述规律,可以推测,当![]() 时,从左往右第22个数为_____________.
时,从左往右第22个数为_____________.
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系中,曲线C1的参数方程为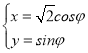 (
(![]() 为参数),以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,直线l的极坐标方程为
为参数),以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,直线l的极坐标方程为![]() ,曲线C2的极坐标方程为ρ=2sinθ.
,曲线C2的极坐标方程为ρ=2sinθ.
(1)探究直线l与曲线C2的位置关系,并说明理由;
(2)若曲线C3的极坐标方程为![]() ,且曲线C3与曲线C1、C2分别交于M、N两点,求|OM|2|ON|2的取值范围.
,且曲线C3与曲线C1、C2分别交于M、N两点,求|OM|2|ON|2的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数f(x)=ex﹣2mx﹣n(0<x<1),其中m,n∈R,e为自然对数的底数.
(1)试讨论函数f(x)的极值;
(2)记函数g(x)=ex﹣mx2﹣nx﹣1(0<x<1),且g(x)的图象在点![]() 处的切的斜率为
处的切的斜率为![]() ,若函数g(x)存在零点,试求实数m的取值范围.
,若函数g(x)存在零点,试求实数m的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知A是圆O:x2+y2=4上一动点,过点A作AB⊥x轴,垂足为B,动点D满足![]() .
.
(1)求动点D的轨迹C的方程;
(2)垂直于x轴的直线M交轨迹C于M、N两点,点P(3,0),直线PM与轨迹C的另一个交点为Q.问:直线NQ是否过一定点?若过定点,求出该定点的坐标;若不过定点,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com