
科目: 来源: 题型:
【题目】如图,在三棱锥![]() 中,顶点
中,顶点![]() 在底面
在底面![]() 上的射影
上的射影![]() 在棱
在棱![]() 上,
上,![]() ,
,![]() ,
,![]() ,
,![]() 为
为![]() 的中点。
的中点。
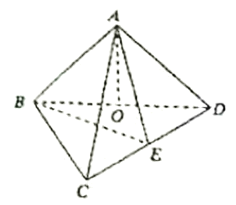
(Ⅰ)求证:![]()
(Ⅱ)求二面角![]() 的余弦值;
的余弦值;
(Ⅲ)已知![]() 是平面
是平面![]() 内一点,点
内一点,点![]() 为
为![]() 中点,且
中点,且![]() 平面
平面![]() ,求线段
,求线段![]() 的长。
的长。
查看答案和解析>>
科目: 来源: 题型:
【题目】高铁和航空的飞速发展不仅方便了人们的出行,更带动了我国经济的巨大发展,据统计,在2018年这一年内从A市到B市乘坐高铁或飞机出行的成年人约为50万人次.为了解乘客出行的满意度,现从中随机抽取100人次作为样本.得到下表(单位:人次):
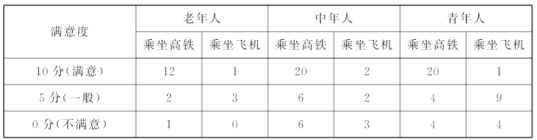
(1)在样本中任取1个,求这个出行人恰好不是青年人的概率;
(2)在2018年从A市到B市乘坐高铁的所有成年人中,随机选取2人次,记其中老年人出行的人次为X.以频率作为概率.求X的分布列和数学期望;
(3)如果甲将要从A市出发到B市,那么根据表格中的数据,你建议甲是乘坐高铁还是 飞机?并说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】在四棱锥S—ABCD中,底面ABCD为长方形,SB⊥底面ABCD,其中BS=2,BA=2,BC=λ,λ的可能取值为:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ;⑤λ=3
;⑤λ=3

(1)求直线AS与平面ABCD所成角的正弦值;
(2)若线段CD上能找到点E,满足AE⊥SE,则λ可能的取值有几种情况?请说明理由;
(3)在(2)的条件下,当λ为所有可能情况的最大值时,线段CD上满足AE⊥SE的点有两个,分别记为E1,E2,求二面角E1-SB-E2的大小.
查看答案和解析>>
科目: 来源: 题型:
【题目】给定椭圆C:![]() (
(![]() ),称圆心在原点O,半径为
),称圆心在原点O,半径为![]() 的圆是椭圆C的“卫星圆”.若椭圆C的离心率
的圆是椭圆C的“卫星圆”.若椭圆C的离心率![]() ,点
,点![]() 在C上.
在C上.
(1)求椭圆C的方程和其“卫星圆”方程;
(2)点P是椭圆C的“卫星圆”上的一个动点,过点P作直线![]() ,
,![]() 使得
使得![]()
![]()
![]() ,与椭圆C都只有一个交点,且
,与椭圆C都只有一个交点,且![]() ,
,![]() 分别交其“卫星圆”于点M,N,证明:弦长
分别交其“卫星圆”于点M,N,证明:弦长![]() 为定值.
为定值.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知菱形ABCD中,∠BAD=60°,AC与BD相交于点O.将△ABD沿BD折起,使顶点A至点M,在折起的过程中,下列结论正确的是( )
A.BD⊥CM
B.存在一个位置,使△CDM为等边三角形
C.DM与BC不可能垂直
D.直线DM与平面BCD所成的角的最大值为60°
查看答案和解析>>
科目: 来源: 题型:
【题目】已知双曲线![]() 的左、右两个顶点分别是A1,A2,左、右两个焦点分别是F1,F2,P是双曲线上异于A1,A2的任意一点,给出下列命题,其中是真命题的有( )
的左、右两个顶点分别是A1,A2,左、右两个焦点分别是F1,F2,P是双曲线上异于A1,A2的任意一点,给出下列命题,其中是真命题的有( )
A.![]()
B.直线![]() 的斜率之积等于定值
的斜率之积等于定值![]()
C.使得![]() 为等腰三角形的点
为等腰三角形的点![]() 有且仅有8个
有且仅有8个
D.![]() 的面积为
的面积为
查看答案和解析>>
科目: 来源: 题型:
【题目】如图是某地某月1日至15日的日平均温度变化的折线图,根据该折线图,下列结论正确的是( )
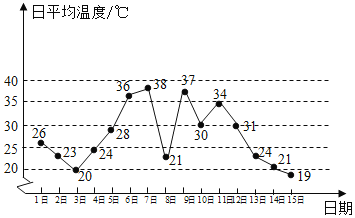
A. 这15天日平均温度的极差为![]()
B. 连续三天日平均温度的方差最大的是7日,8日,9日三天
C. 由折线图能预测16日温度要低于![]()
D. 由折线图能预测本月温度小于![]() 的天数少于温度大于
的天数少于温度大于![]() 的天数
的天数
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com