
科目: 来源: 题型:
【题目】某调研机构,对本地![]() 岁的人群随机抽取
岁的人群随机抽取![]() 人进行了一次生活习惯是否符合低碳观念的调查,将生活习惯符合低碳观念的称为“低碳族”,否则称为“非低碳族”,结果显示,有
人进行了一次生活习惯是否符合低碳观念的调查,将生活习惯符合低碳观念的称为“低碳族”,否则称为“非低碳族”,结果显示,有![]() 人为“低碳族”,该
人为“低碳族”,该![]() 人的年龄情况对应的频率分布直方图如图.
人的年龄情况对应的频率分布直方图如图.
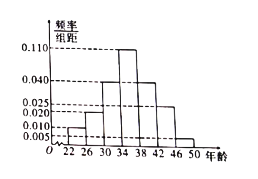
(1)根据频率分布直方图,估计这![]() 名“低碳族”年龄的平均值,中位数;
名“低碳族”年龄的平均值,中位数;
(2)若在“低碳族”且年龄在![]() 、
、![]() 的两组人群中,用分层抽样的方法抽取
的两组人群中,用分层抽样的方法抽取![]() 人,试估算每个年龄段应各抽取多少人?
人,试估算每个年龄段应各抽取多少人?
查看答案和解析>>
科目: 来源: 题型:
【题目】阿波罗尼斯(约公元前![]() 年)证明过这样一个命题:平面内到两定点距离之比为常数
年)证明过这样一个命题:平面内到两定点距离之比为常数![]() 的点的轨迹是圆,后人将这个圆称为阿波罗尼斯圆.若平面内两定点
的点的轨迹是圆,后人将这个圆称为阿波罗尼斯圆.若平面内两定点![]() 、
、![]() 间的距离为
间的距离为![]() ,动点
,动点![]() 满足
满足![]() ,则
,则![]() 的最小值为( )
的最小值为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】每年六、七月份,我国长江中下游地区进入持续25天左右的梅雨季节,如图是江南某地区![]() 年10年间梅雨季节的降雨量
年10年间梅雨季节的降雨量![]() 单位:
单位:![]() 的频率分布直方图,试用样本频率估计总体概率,解答下列问题:
的频率分布直方图,试用样本频率估计总体概率,解答下列问题:

![]() 假设每年的梅雨季节天气相互独立,求该地区未来三年里至少有两年梅雨季节的降雨量超过350mm的概率.
假设每年的梅雨季节天气相互独立,求该地区未来三年里至少有两年梅雨季节的降雨量超过350mm的概率.
![]() 老李在该地区承包了20亩土地种植杨梅,他过去种植的甲品种杨梅,平均每年的总利润为28万元
老李在该地区承包了20亩土地种植杨梅,他过去种植的甲品种杨梅,平均每年的总利润为28万元![]() 而乙品种杨梅的亩产量
而乙品种杨梅的亩产量![]() 亩
亩![]() 与降雨量之间的关系如下面统计表所示,又知乙品种杨梅的单位利润为
与降雨量之间的关系如下面统计表所示,又知乙品种杨梅的单位利润为![]() 元
元![]() ,请你帮助老李分析,他来年应该种植哪个品种的杨梅可以使总利润
,请你帮助老李分析,他来年应该种植哪个品种的杨梅可以使总利润![]() 万元
万元![]() 的期望更大?并说明理由.
的期望更大?并说明理由.
降雨量 |
|
|
|
|
亩产量 | 500 | 700 | 600 | 400 |
查看答案和解析>>
科目: 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为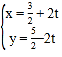 (
(![]() 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,![]() 轴正半轴为极轴建立极坐标系.曲线
轴正半轴为极轴建立极坐标系.曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的普通方程,曲线
的普通方程,曲线![]() 的参数方程;
的参数方程;
(2)若![]() 分别为曲线
分别为曲线![]() ,
,![]() 上的动点,求
上的动点,求![]() 的最小值,并求
的最小值,并求![]() 取得最小值时,
取得最小值时,![]() 点的直角坐标.
点的直角坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知点![]() ,直线
,直线![]() 为平面内的动点,过点
为平面内的动点,过点![]() 作直线
作直线![]() 的垂线,垂足为点
的垂线,垂足为点![]() ,且
,且![]() .
.
(1)求动点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)过点![]() 作两条互相垂直的直线
作两条互相垂直的直线![]() 与
与![]() 分别交轨迹
分别交轨迹![]() 于
于![]() 四点.求
四点.求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】某城市为了解游客人数的变化规律,提高旅游服务质量,收集并整理了2017年1月至2019年12月期间月接待游客量(单位:万人)的数据,绘制了下面的折线图.根据该折线图,下列结论错误的是( )
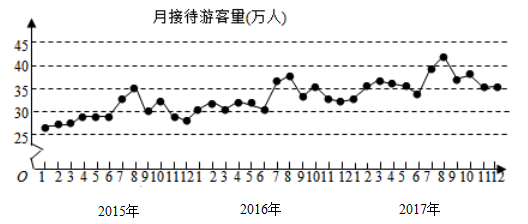
A.年接待游客量逐年增加
B.各年的月接待游客量高峰期大致在8月
C.2017年1月至12月月接待游客量的中位数为30万人
D.各年1月至6月的月接待游客量相对于7月至12月,波动性更小,变化比较平稳
查看答案和解析>>
科目: 来源: 题型:
【题目】已知![]() ,
,![]() 为椭圆E:
为椭圆E:![]() 的左、右焦点,过点
的左、右焦点,过点![]() 的直线l与椭圆E有且只有一个交点T.
的直线l与椭圆E有且只有一个交点T.
(1)求![]() 面积的取值范围.
面积的取值范围.
(2)若有一束光线从点![]() 射出,射在直线l上的T点上,经过直线l反射后,试问反射光线是否恒过定点?若是,请求出该定点;若否,请说明理由.
射出,射在直线l上的T点上,经过直线l反射后,试问反射光线是否恒过定点?若是,请求出该定点;若否,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】随着银行业的不断发展,市场竞争越来越激烈,顾客对银行服务质量的要求越来越高,银行为了提高柜员员工的服务意识,加强评价管理,工作中让顾客对服务作出评价,评价分为满意、基本满意、不满意三种.某银行为了比较顾客对男女柜员员工满意度评价的差异,在下属的四个分行中随机抽出40人(男女各半)进行分析比较.对40人一月中的顾客评价“不满意”的次数进行了统计,按男、女分为两组,再将每组柜员员工的月“不满意”次数分为5组:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,得到如下频数分布表.
,得到如下频数分布表.
分组 |
|
|
|
|
|
女柜员 | 2 | 3 | 8 | 5 | 2 |
男柜员 | 1 | 3 | 9 | 4 | 3 |
(1)在答题卡所给的坐标系中分别画出男、女柜员员工的频率分布直方图;分别求出男、女柜员员工的月平均“不满意”次数的估计值,试根据估计值比较男、女柜员员工的满意度谁高?
(2)在抽取的40名柜员员工中:从“不满意”次数不少于20的员工中随机抽取3人,并用X表示随机抽取的3人中女柜员工的人数,求X的分布列和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com