
科目: 来源: 题型:
【题目】要排出高三某班一天中,语文、数学、英语各![]() 节,自习课
节,自习课![]() 节的功课表,其中上午
节的功课表,其中上午![]() 节,下午
节,下午![]() 节,若要求
节,若要求![]() 节语文课必须相邻且
节语文课必须相邻且![]() 节数学课也必须相邻(注意:上午第五节和下午第一节不算相邻),则不同的排法种数是( )
节数学课也必须相邻(注意:上午第五节和下午第一节不算相邻),则不同的排法种数是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】古人云:“腹有诗书气自华.”为响应全民阅读,建设书香中国,校园读书活动的热潮正在兴起.某校为统计学生一周课外读书的时间,从全校学生中随机抽取![]() 名学生进行问卷调査,统计了他们一周课外读书时间(单位:
名学生进行问卷调査,统计了他们一周课外读书时间(单位:![]() )的数据如下:
)的数据如下:
一周课外读书时间/ |
|
|
|
|
|
|
|
|
| 合计 |
频数 | 4 | 6 | 10 | 12 | 14 | 24 |
| 46 | 34 |
|
频率 | 0.02 | 0.03 | 0.05 | 0.06 | 0.07 | 0.12 | 0.25 |
| 0.17 | 1 |
(1)根据表格中提供的数据,求![]() ,
,![]() ,
,![]() 的值并估算一周课外读书时间的中位数.
的值并估算一周课外读书时间的中位数.
(2)如果读书时间按![]() ,
,![]() ,
,![]() 分组,用分层抽样的方法从
分组,用分层抽样的方法从![]() 名学生中抽取20人.
名学生中抽取20人.
①求每层应抽取的人数;
②若从![]() ,
,![]() 中抽出的学生中再随机选取2人,求这2人不在同一层的概率.
中抽出的学生中再随机选取2人,求这2人不在同一层的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知在三棱台![]() 中,
中,![]() ,
,![]() ,
,![]() .
.
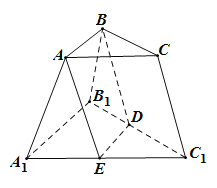
(1)求证:![]() ;
;
(2)过![]() 的平面
的平面![]() 分别交
分别交![]() ,
,![]() 于点
于点![]() ,
,![]() ,且分割三棱台
,且分割三棱台![]() 所得两部分几何体的体积比为
所得两部分几何体的体积比为![]() ,几何体
,几何体![]() 为棱柱,求
为棱柱,求![]() 的长.
的长.
提示:台体的体积公式![]() (
(![]() ,
,![]() 分别为棱台的上、下底面面积,
分别为棱台的上、下底面面积,![]() 为棱台的高).
为棱台的高).
查看答案和解析>>
科目: 来源: 题型:
【题目】如图1,在梯形ABCD中,AB//CD,AB=3,CD=6,过A,B分别作CD的垂线,垂足分别为E,F,已知DE=1,AE=3,将梯形ABCD沿AE,BF同侧折起,使得平面ADE⊥平面ABFE,平面ADE∥平面BCF,得到图2.
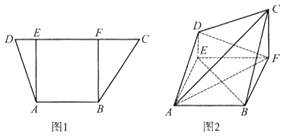
(1)证明:BE//平面ACD;
(2)求三棱锥C﹣AED的体积.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知一个正四面体纸盒的俯视图如图所示,其中四边形ABCD是边长为![]() 的正方形,若在该正四面体纸盒内放一个正方体,使正方体可以在纸盒内任意转动,则正方体棱长的最大值是_____.
的正方形,若在该正四面体纸盒内放一个正方体,使正方体可以在纸盒内任意转动,则正方体棱长的最大值是_____.
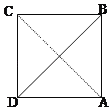
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的离心率为
的离心率为![]() ,且与抛物线
,且与抛物线![]() 交于
交于![]() ,
,![]() 两点,
两点,![]() (
(![]() 为坐标原点)的面积为
为坐标原点)的面积为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)如图,点![]() 为椭圆上一动点(非长轴端点)
为椭圆上一动点(非长轴端点)![]() ,
,![]() 为左、右焦点,
为左、右焦点,![]() 的延长线与椭圆交于
的延长线与椭圆交于![]() 点,
点,![]() 的延长线与椭圆交于
的延长线与椭圆交于![]() 点,求
点,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目: 来源: 题型:
【题目】树立和践行“绿水青山就是金山银山,坚持人与自然和谐共生”的理念越来越深入人心,已形成了全民自觉参与,造福百姓的良性循环.据此,某网站退出了关于生态文明建设进展情况的调查,调查数据表明,环境治理和保护问题仍是百姓最为关心的热点,参与调查者中关注此问题的约占![]() .现从参与关注生态文明建设的人群中随机选出200人,并将这200人按年龄分组:第1组
.现从参与关注生态文明建设的人群中随机选出200人,并将这200人按年龄分组:第1组![]() ,第2组
,第2组![]() ,第3组
,第3组![]() ,第4组
,第4组![]() ,第5组
,第5组![]() ,得到的频率分布直方图如图所示.
,得到的频率分布直方图如图所示.

(I)求出![]() 的值;
的值;
(II)求出这200人年龄的样本平均数(同一组数据用该区间的中点值作代表)和中位数(精确到小数点后一位);
(III)现在要从年龄较小的第1,2组中用分层抽样的方法抽取5人,再从这5人中随机抽取3人进行问卷调查,求第2组恰好抽到2人的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】随着科技的发展,网络已逐渐融入了人们的生活.网购是非常方便的购物方式,为了了解网购在我市的普及情况,某调查机构进行了有关网购的调查问卷,并从参与调查的市民中随机抽取了男女各100人进行分析,从而得到表(单位:人)
经常网购 | 偶尔或不用网购 | 合计 | |
男性 | 50 | 100 | |
女性 | 70 | 100 | |
合计 |
(1)完成上表,并根据以上数据判断能否在犯错误的概率不超过0.01的前提下认为我市市民网购与性别有关?
(2)①现从所抽取的女市民中利用分层抽样的方法抽取10人,再从这10人中随机选取3人赠送优惠券,求选取的3人中至少有2人经常网购的概率;
②将频率视为概率,从我市所有参与调查的市民中随机抽取10人赠送礼品,记其中经常网购的人数为![]() ,求随机变量
,求随机变量![]() 的数学期望和方差.
的数学期望和方差.
参考公式: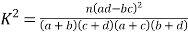
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com