
科目: 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为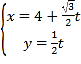 (
(![]() 为参数).以坐标原点为极点,
为参数).以坐标原点为极点,![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]()
(1)在曲线![]() 上任取一点
上任取一点![]() ,连接
,连接![]() ,在射线
,在射线![]() 上取一点
上取一点![]() ,使
,使![]() ,求
,求![]() 点轨迹的极坐标方程;
点轨迹的极坐标方程;
(2)在曲线![]() 上任取一点
上任取一点![]() ,在曲线
,在曲线![]() 上任取一点
上任取一点![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目: 来源: 题型:
【题目】定义:若函数![]() 的导函数
的导函数![]() 是奇函数(
是奇函数(![]() ),则称函数
),则称函数![]() 是“双奇函数” .函数
是“双奇函数” .函数![]() .
.
(1)若函数![]() 是“双奇函数”,求实数
是“双奇函数”,求实数![]() 的值;
的值;
(2)假设![]() .
.
(i)在(1)的条件下,讨论函数![]() 的单调性;
的单调性;
(ii)若![]() ,讨论函数
,讨论函数![]() 的极值点.
的极值点.
查看答案和解析>>
科目: 来源: 题型:
【题目】“微信运动”已成为当下热门的运动方式,小王的微信朋友内也有大量好友参与了“微信运动”,他随机选取了其中的40人(男、女各20人),记录了他们某一天的走路步数,并将数据整理如下:
性别 步数 | 0~2000 | 2001~5000 | 5001~8000 | 8001~10000 | >10000 |
男 | 1 | 2 | 3 | 6 | 8 |
女 | 0 | 2 | 10 | 6 | 2 |
(1)已知某人一天的走路步数超过8000步被系统评定为“积极型”,否则为“懈怠型”,根据题意完成下面的2×2列联表,并据此判断能否有95%以上的把握认为“评定类型”与“性别”有关?
积极型 | 懈怠型 | 总计 | |
男 | |||
女 | |||
总计 |
(2)若小王以这40位好友该日走路步数的频率分布来估计其所有微信好友每日走路步数的概率分布,现从小王的所有微信好友中任选2人,其中每日走路不超过5000步的有X人,超过10000步的有Y人,设ξ=|X﹣Y|,求E的分布列及数学期望.
附:K2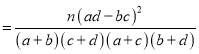 ,n=a+b+c+d.
,n=a+b+c+d.
P(K2≥k0) | 0.10 | 0.05 | 0.025 | 0.010 |
k0 | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,短轴长为
,短轴长为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若椭圆![]() 的左焦点为
的左焦点为![]() ,过点
,过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,则在
两点,则在![]() 轴上是否存在一个定点
轴上是否存在一个定点![]() 使得直线
使得直线![]() 的斜率互为相反数?若存在,求出定点
的斜率互为相反数?若存在,求出定点![]() 的坐标;若不存在,也请说明理由.
的坐标;若不存在,也请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数![]() ,
,![]() .
.
(1)若对![]() 时,不等式
时,不等式![]() 恒成立,求实数a的取值范围(e为自然对数的底数);
恒成立,求实数a的取值范围(e为自然对数的底数);
(2)当![]() 时,求函数
时,求函数![]() 的极大值;
的极大值;
(3)求证:当![]() 时,曲线
时,曲线![]() 与直线
与直线![]() 有且仅有一个公共点.
有且仅有一个公共点.
查看答案和解析>>
科目: 来源: 题型:
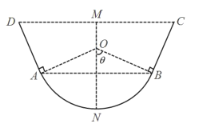
【题目】某农场计划设计建造一条2000米长的水渠,其横断面如图所示.其中,底部是半径为1米的圆弧![]() ,上部是有一定倾角的线段
,上部是有一定倾角的线段![]() 与
与![]() ,渠深
,渠深![]() 为
为![]() 米,且圆弧
米,且圆弧![]() 的圆心为O在
的圆心为O在![]() 上,
上,![]() ,
,![]() ,
,![]() ,
,![]() .据测算,水渠底部曲面每平方米的造价为
.据测算,水渠底部曲面每平方米的造价为![]() 百元,上部矩形壁面每平方米的造价为1百元,其他费用忽略不计.设
百元,上部矩形壁面每平方米的造价为1百元,其他费用忽略不计.设![]() ,
,![]() .
.
(1)试用![]() 表示水渠建造的总费用
表示水渠建造的总费用![]() (单位:百元);
(单位:百元);
(2)试确定![]() 的值,使得建造总费用最低.
的值,使得建造总费用最低.
查看答案和解析>>
科目: 来源: 题型:
【题目】某中学为了丰富学生的课外文体活动,分别开设了阅读、书法、绘画等文化活动;跑步、游泳、健身操等体育活动.该中学共有高一学生300名,要求每位学生必须选择参加其中一项活动,现对高一学生的性别、学习积极性及选择参加的文体活动情况进行统计,得到数据如下:

(1)在选择参加体育活动的学生中按性别分层抽取6名,再从这6名学生中抽取2人了解家庭情况,求2人中至少有1名女生的概率;
(2)是否有99.9%的把握认为学生的学习积极性与选择参加文化活动有关?请说明你的理由.
附:参考公式:![]() ,其中
,其中![]() .
.

查看答案和解析>>
科目: 来源: 题型:
【题目】选修4-4:坐标系与参数方程:在平面直角坐标系![]() 中,曲线
中,曲线![]() :
:![]() (
(![]() 为参数),在以平面直角坐标系的原点为极点、
为参数),在以平面直角坐标系的原点为极点、![]() 轴的正半轴为极轴,且与平面直角坐标系
轴的正半轴为极轴,且与平面直角坐标系![]() 取相同单位长度的极坐标系中,曲线
取相同单位长度的极坐标系中,曲线![]() :
:![]() .
.
(1)求曲线![]() 的普通方程以及曲线
的普通方程以及曲线![]() 的平面直角坐标方程;
的平面直角坐标方程;
(2)若曲线![]() 上恰好存在三个不同的点到曲线
上恰好存在三个不同的点到曲线![]() 的距离相等,求这三个点的极坐标.
的距离相等,求这三个点的极坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com