
科目: 来源: 题型:
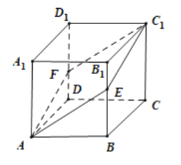
【题目】如图,在正方体![]() 中,点
中,点![]() 为棱
为棱![]() 上一动点(不包括顶点),平面
上一动点(不包括顶点),平面![]() 交
交![]() 于点
于点![]() ,则下列结论中错误的是( )
,则下列结论中错误的是( )
A.存在点![]() ,使得四边形
,使得四边形![]() 为菱形
为菱形
B.存在点![]() ,使得四边形
,使得四边形![]() 的面积最小
的面积最小
C.存在点![]() ,使得
,使得![]() 平面
平面![]()
D.存在点![]() ,使得平面
,使得平面![]() 平面
平面![]() (其中
(其中![]() 为
为![]() 的中点)
的中点)
查看答案和解析>>
科目: 来源: 题型:
【题目】已知正项数列![]() 满足:
满足:![]() ,
,![]() ,其中
,其中![]() .
.
(1)若![]() ,求数列
,求数列![]() 的前
的前![]() 项的和;
项的和;
(2)若![]() ,
,![]() .
.
①求数列![]() 的通项公式;
的通项公式;
②记数列![]() 的前
的前![]() 项的和为
项的和为![]() ,若无穷项等比数列
,若无穷项等比数列![]() 始终满足
始终满足![]() ,求数列
,求数列![]() 的通项公式.
的通项公式.
查看答案和解析>>
科目: 来源: 题型:
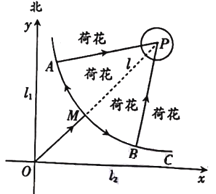
【题目】如图,某市建有贯穿东西和南北的两条垂直公路![]() ,
,![]() ,在它们交叉路口点
,在它们交叉路口点![]() 处的东北方向建有一个荷花池,荷花池的外围是一条环形公路,荷花池中的固定观景台
处的东北方向建有一个荷花池,荷花池的外围是一条环形公路,荷花池中的固定观景台![]() 位于两条垂直公路的角平分线
位于两条垂直公路的角平分线![]() 上,
上,![]() 与环形公路的交点记作
与环形公路的交点记作![]() .游客游览荷花池时,需沿公路
.游客游览荷花池时,需沿公路![]() 先到达环形公路
先到达环形公路![]() 处.为了分流游客,方便游客游览荷花池,计划从靠近公路
处.为了分流游客,方便游客游览荷花池,计划从靠近公路![]() ,
,![]() 的环形公路上选
的环形公路上选![]() ,
,![]() 两处(
两处(![]() ,
,![]() 关于直线
关于直线![]() 对称)修建直达观景台
对称)修建直达观景台![]() 的玻璃栈道
的玻璃栈道![]() ,
,![]() .以
.以![]() ,
,![]() 所在的直线为
所在的直线为![]() ,
,![]() 轴建立平面直角坐标系
轴建立平面直角坐标系![]() ,靠近公路
,靠近公路![]() ,
,![]() 的环形公路可用曲线
的环形公路可用曲线![]() 近似表示,曲线
近似表示,曲线![]() 符合函数
符合函数![]() .
.
(1)若![]() 百米,点
百米,点![]() 到
到![]() 的垂直距离为1百米,求玻璃栈道
的垂直距离为1百米,求玻璃栈道![]() 的总长度;
的总长度;
(2)若要使得玻璃栈道![]() 的总长度最小为
的总长度最小为![]() 百米,求观景台
百米,求观景台![]() 的位置.
的位置.
查看答案和解析>>
科目: 来源: 题型:
【题目】某商店销售某海鲜,统计了春节前后50天该海鲜的需求量![]() (
(![]() ,单位:公斤),其频率分布直方图如图所示,该海鲜每天进货1次,商店每销售1公斤可获利50元;若供大于求,剩余的削价处理,每处理1公斤亏损10元;若供不应求,可从其它商店调拨,销售1公斤可获利30元.假设商店每天该海鲜的进货量为14公斤,商店的日利润为
,单位:公斤),其频率分布直方图如图所示,该海鲜每天进货1次,商店每销售1公斤可获利50元;若供大于求,剩余的削价处理,每处理1公斤亏损10元;若供不应求,可从其它商店调拨,销售1公斤可获利30元.假设商店每天该海鲜的进货量为14公斤,商店的日利润为![]() 元.
元.

(1)求商店日利润![]() 关于需求量
关于需求量![]() 的函数表达式;
的函数表达式;
(2)假设同组中的每个数据用该组区间的中点值代替.
①求这50天商店销售该海鲜日利润的平均数;
②估计日利润在区间![]() 内的概率.
内的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】某盒子中有4个小球,分别写有“中”、“美”、“建”、“交”四个字,从中任取一个小球,有放回抽取,直到“建”、“交”二字都取到就停止,用随机模拟的方法估计恰好在第三次停止的概率;利用电脑随机产生0到3之间取整数值的随机数,分别用0,1,2,3,代表“中”、“美”、“建”、“交”着四个字,以每三个随机数为一组,表示取球三次的结果,经随机模拟产生了一下18组随机数:
323 213 320 032 132 031 123 330 110
321 120 122 321 221 230 132 322 130
由此可以估计,恰好第三次停止的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】2018年9~12月某市邮政快递业务量完成件数较2017年9~12月同比增长25%,该市2017年9~12月邮政快递业务量柱形图及2018年9~12月邮政快递业务量结构扇形图如图所示,根据统计图,给出下列结论:
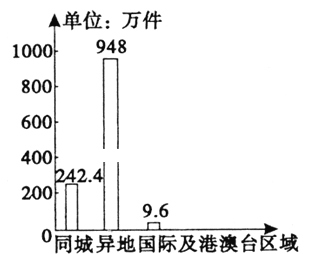
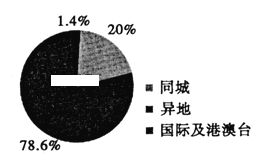
①2018年9~12月,该市邮政快递业务量完成件数约1500万件;
②2018年9~12月,该市邮政快递同城业务量完成件数与2017年9~12月相比有所减少;
③2018年9~12月,该市邮政快递国际及港澳台业务量同比增长超过75%,其中正确结论的个数为( )
A. 3
B. 2
C. 1
D. 0
查看答案和解析>>
科目: 来源: 题型:
【题目】已知某地区某种昆虫产卵数和温度有关.现收集了一只该品种昆虫的产卵数![]() (个)和温度
(个)和温度![]() (
(![]() )的7组观测数据,其散点图如所示:
)的7组观测数据,其散点图如所示:
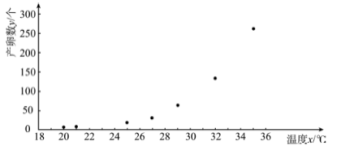
根据散点图,结合函数知识,可以发现产卵数![]() 和温度
和温度![]() 可用方程
可用方程![]() 来拟合,令
来拟合,令![]() ,结合样本数据可知
,结合样本数据可知![]() 与温度
与温度![]() 可用线性回归方程来拟合.根据收集到的数据,计算得到如下值:
可用线性回归方程来拟合.根据收集到的数据,计算得到如下值:
|
|
|
|
|
|
27 | 74 |
| 182 |
|
|
表中![]() ,
,![]() .
.
(1)求![]() 和温度
和温度![]() 的回归方程(回归系数结果精确到
的回归方程(回归系数结果精确到![]() );
);
(2)求产卵数![]() 关于温度
关于温度![]() 的回归方程;若该地区一段时间内的气温在
的回归方程;若该地区一段时间内的气温在![]() 之间(包括
之间(包括![]() 与
与![]() ),估计该品种一只昆虫的产卵数的范围.(参考数据:
),估计该品种一只昆虫的产卵数的范围.(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .)
.)
附:对于一组数据![]() ,
,![]() ,…,
,…,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com