
科目: 来源: 题型:
【题目】已知直线![]() 的参数方程是
的参数方程是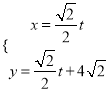 (
(![]() 是参数),以坐标原点为原点,
是参数),以坐标原点为原点, ![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)判断直线![]() 与曲线
与曲线![]() 的位置关系;
的位置关系;
(2)过直线![]() 上的点作曲线
上的点作曲线![]() 的切线,求切线长的最小值.
的切线,求切线长的最小值.
查看答案和解析>>
科目: 来源: 题型:
【题目】某校为研究学生语言学科的学习情况,现对高二200名学生英语和语文某次考试成绩进行抽样分析.将200名学生编号为001,002,…,200,采用系统抽样的方法等距抽取10名学生,将10名学生的两科成绩(单位:分)绘成折线图如下:
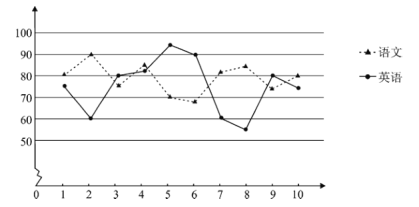
(1)若第二段抽取的学生编号是026,写出第六段抽取的学生编号;
(2)在这两科成绩差低于20分的学生中随机抽取2人进行访谈,求2人成绩均是语文成绩高于英语成绩的概率;
(3)根据折线图,比较该校高二年级学生的语文和英语两科成绩,写出至少两条统计结论.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在几何体![]() 中,底面
中,底面![]() 为矩形,
为矩形,![]() ,
,![]() ,
,![]() ,
,![]() .
.![]() 为棱
为棱![]() 上一点,平面
上一点,平面![]() 与棱
与棱![]() 交于点
交于点![]() .
.
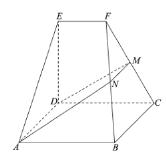
(1)求证:![]() ;
;
(2)若![]() ,试问平面
,试问平面![]() 是否可能与平面
是否可能与平面![]() 垂直?若能,求出
垂直?若能,求出![]() 的值;若不能,说明理由.
的值;若不能,说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】设圆![]() 的圆心为
的圆心为![]() ,直线
,直线![]() 过点
过点![]() 且与
且与![]() 轴不重合,
轴不重合, ![]() 交圆
交圆![]() 于
于![]() 两点,过
两点,过![]() 作
作![]() 的平行线交
的平行线交![]() 于点
于点![]() .
.
(1)证明![]() 为定值,并写出点
为定值,并写出点![]() 的轨迹方程;
的轨迹方程;
(2)设![]() ,过点
,过点![]() 作直线
作直线![]() ,交点
,交点![]() 的轨迹于
的轨迹于![]() 两点 (异于
两点 (异于![]() ),直线
),直线![]() 的斜率分别为
的斜率分别为![]() ,证明:
,证明: ![]() 为定值.
为定值.
查看答案和解析>>
科目: 来源: 题型:
【题目】在测试中,客观题难度的计算公式为![]() ,其中
,其中![]() 为第
为第![]() 题的难度,
题的难度,![]() 为答对该题的人数,
为答对该题的人数,![]() 为参加测试的总人数.现对某校高三年级240名学生进行一次测试,共5道客观题.测试前根据对学生的了解,预估了每道题的难度,如下表所示:
为参加测试的总人数.现对某校高三年级240名学生进行一次测试,共5道客观题.测试前根据对学生的了解,预估了每道题的难度,如下表所示:
题号 | 1 | 2 | 3 | 4 | 5 |
考前预估难度 | 0.9 | 0.8 | 0.7 | 0.6 | 0.4 |
测试后,随机抽取了20名学生的答题数据进行统计,结果如下:
题号 | 1 | 2 | 3 | 4 | 5 |
实测答对人数 | 16 | 16 | 14 | 14 | 8 |