
科目: 来源: 题型:
【题目】在本题中,我们把具体如下性质的函数![]() 叫做区间
叫做区间![]() 上的闭函数:①
上的闭函数:①![]() 的定义域和值域都是
的定义域和值域都是![]() ;②
;②![]() 在
在![]() 上是增函数或者减函数.
上是增函数或者减函数.
(1)若![]() 在区间
在区间![]() 上是闭函数,求常数
上是闭函数,求常数![]() 的值;
的值;
(2)找出所有形如![]() 的函数(
的函数(![]() 都是常数),使其在区间
都是常数),使其在区间![]() 上是闭函数.
上是闭函数.
查看答案和解析>>
科目: 来源: 题型:
【题目】某市计划在一片空地上建一个集购物、餐饮、娱乐为一体的大型综合园区,如图,已知两个购物广场的占地都呈正方形,它们的面积分别为13公顷和8公顷;美食城和欢乐大世界的占地也都呈正方形,分别记它们的面积为![]() 公顷和
公顷和![]() 公顷;由购物广场、美食城和欢乐大世界围成的两块公共绿地都呈三角形,分别记它们的面积为
公顷;由购物广场、美食城和欢乐大世界围成的两块公共绿地都呈三角形,分别记它们的面积为![]() 公顷和
公顷和![]() 公顷.
公顷.
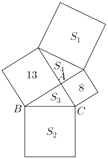
(1)设![]() ,用关于
,用关于![]() 的函数
的函数![]() 表示
表示![]() ,并求
,并求![]() 在区间
在区间![]() 上的最大值的近似值(精确到0.001公顷);
上的最大值的近似值(精确到0.001公顷);
(2)如果![]() ,并且
,并且![]() ,试分别求出
,试分别求出![]() 、
、![]() 、
、![]() 、
、![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】某中学拟在高一下学期开设游泳选修课,为了了解高一学生喜欢游泳是否与性别有关,该学校对100名高一新生进行了问卷调查,得到如下列联表:
喜欢游泳 | 不喜欢游泳 | 合计 | |
男生 | 10 | ||
女生 | 20 | ||
合计 |
已知在这100人中随机抽取1人抽到喜欢游泳的学生的概率为![]() .
.
(1)请将上述列联表补充完整;
(2)并判断是否有99.9%的把握认为喜欢游泳与性别有关?并说明你的理由;
(3)已知在被调查的学生中有5名来自甲班,其中3名喜欢游泳,现从这5名学生中随机抽取2人,求恰好有1人喜欢游泳的概率.
下面的临界值表仅供参考:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(参考公式: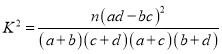 ,其中
,其中![]() )
)
查看答案和解析>>
科目: 来源: 题型:
【题目】某地区试行高考考试改革:在高三学年中举行5次统一测试,学生如果通过其中2次测试即可获得足够学分升上大学继续学习,不用参加其余的测试,而每个学生最多也只能参加5次测试![]() 假设某学生每次通过测试的概率都是
假设某学生每次通过测试的概率都是![]() ,每次测试时间间隔恰当,每次测试通过与否互相独立.
,每次测试时间间隔恰当,每次测试通过与否互相独立.
(1)求该学生考上大学的概率.
(2)如果考上大学或参加完5次测试就结束,记该生参加测试的次数为X,求X的概率分布及X的数学期望.
查看答案和解析>>
科目: 来源: 题型:
【题目】如果无穷数列{an}满足条件:①![]() ;② 存在实数M,使得an≤M,其中n∈N*,那么我们称数列{an}为Ω数列.
;② 存在实数M,使得an≤M,其中n∈N*,那么我们称数列{an}为Ω数列.
(1)设数列{bn}的通项为bn=20n-2n,且是Ω数列,求M的取值范围;
(2)设{cn}是各项为正数的等比数列,Sn是其前n项和,c3=![]() ,S3=
,S3=![]() ,证明:数列{Sn}是Ω数列;
,证明:数列{Sn}是Ω数列;
(3)设数列{dn}是各项均为正整数的Ω数列,求证:dn≤dn+1.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数![]()
(1)若![]() ,求
,求![]() 的最大值;
的最大值;
(2)如果函数![]() 在公共定义域D上,满足
在公共定义域D上,满足![]() ,那么就称
,那么就称![]() 为
为![]() 的“伴随函数”.已知函数
的“伴随函数”.已知函数![]() ,
,![]() .若在区间
.若在区间![]() 上,函数
上,函数![]() 是
是![]() 的“伴随函数”,求实数
的“伴随函数”,求实数![]() 的取值范围;
的取值范围;
(3)若![]() ,正实数
,正实数![]() 满足
满足![]() ,证明:
,证明:![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图是一幅招贴画的示意图,其中ABCD是边长为![]() 的正方形,周围是四个全等的弓形.已知O为正方形的中心,G为AD的中点,点P在直线OG上,弧AD是以P为圆心、PA为半径的圆的一部分,OG的延长线交弧AD于点H.设弧AD的长为
的正方形,周围是四个全等的弓形.已知O为正方形的中心,G为AD的中点,点P在直线OG上,弧AD是以P为圆心、PA为半径的圆的一部分,OG的延长线交弧AD于点H.设弧AD的长为![]() ,
,![]() .
.
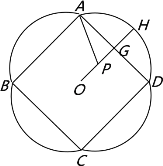
(1)求![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(2)定义比值![]() 为招贴画的优美系数,当优美系数最大时,招贴画最优美.证明:当角
为招贴画的优美系数,当优美系数最大时,招贴画最优美.证明:当角![]() 满足:
满足:![]() 时,招贴画最优美.
时,招贴画最优美.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com