
科目: 来源: 题型:
【题目】“割圆术”是刘徽最突出的数学成就之一,他在《九章算术注》中提出割圆术,并作为计算圆的周长,面积已经圆周率的基础,刘徽把圆内接正多边形的面积一直算到了正3072边形,并由此而求得了圆周率为3.1415和3.1416这两个近似数值,这个结果是当时世界上圆周率计算的最精确数据.如图,当分割到圆内接正六边形时,某同学利用计算机随机模拟法向圆内随机投掷点,计算得出该点落在正六边形内的频率为0.8269,那么通过该实验计算出来的圆周率近似值为(参考数据:![]() )
)

A. 3.1419B. 3.1417C. 3.1415D. 3.1413
查看答案和解析>>
科目: 来源: 题型:
【题目】自由购是一种通过自助结算购物的形式.某大型超市为调查顾客自由购的使用情况,随机抽取了100人,调查结果整理如下:
20以下 | [20,30) | [30,40) | [40,50) | [50,60) | [60,70] | 70以上 | |
使用人数 | 3 | 12 | 17 | 6 | 4 | 2 | 0 |
未使用人数 | 0 | 0 | 3 | 14 | 36 | 3 | 0 |
(1)现随机抽取1名顾客,试估计该顾客年龄在[30,50)且未使用自由购的概率;
(2)从被抽取的年龄在[50,70]使用的自由购顾客中,随机抽取2人进一步了解情况,求这2人年龄都在[50,60)的概率;
(3)为鼓励顾客使用自由购,该超市拟对使用自由购顾客赠送1个环保购物袋.若某日该超市预计有5000人购物,试估计该超市当天至少应准备多少个环保购物袋?
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,![]() 轴正半轴为极轴,建立极坐标系,已知曲线
轴正半轴为极轴,建立极坐标系,已知曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的普通方程与曲线
的普通方程与曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)设点![]() ,直线
,直线![]() 与曲线
与曲线![]() 交于不同的两点
交于不同的两点![]() 、
、![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图空间几何体![]() 中,
中,![]() 与
与![]() ,
,![]() 均为边长为
均为边长为![]() 的等边三角形,平面
的等边三角形,平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() .
.
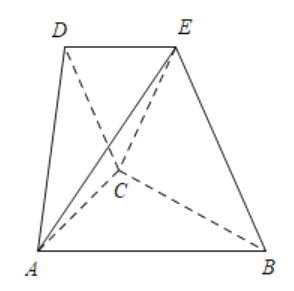
(Ⅰ)求线段![]() 的长度.
的长度.
(Ⅱ)试在平面![]() 内作一条直线,使得直线上任意一点
内作一条直线,使得直线上任意一点![]() 与
与![]() 的连线
的连线![]() 均与平面
均与平面![]() 平行,并给出详细证明;
平行,并给出详细证明;
查看答案和解析>>
科目: 来源: 题型:
【题目】第十三届全国人民代表大会第二次会议和政协第十三届全国委员会第二次会议(简称两会)将分别于![]() 年
年![]() 月
月![]() 日和
日和![]() 月
月![]() 日在北京开幕.全国两会召开前夕,某网站推出两会热点大型调查,调查数据表明,网约车安全问题是百姓最为关心的热点之一,参与调查者中关注此问题的约占
日在北京开幕.全国两会召开前夕,某网站推出两会热点大型调查,调查数据表明,网约车安全问题是百姓最为关心的热点之一,参与调查者中关注此问题的约占![]() .现从参与者中随机选出
.现从参与者中随机选出![]() 人,并将这
人,并将这![]() 人按年龄分组:第
人按年龄分组:第![]() 组
组![]() ,第
,第![]() 组
组![]() ,第
,第![]() 组
组![]() ,第
,第![]() 组
组![]() ,第
,第![]() 组
组![]() ,得到的频率分布直方图如图所示:
,得到的频率分布直方图如图所示:
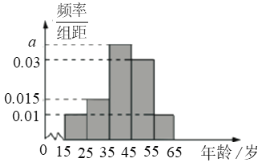
(Ⅰ)现在要从年龄较小的第![]() ,
,![]() 组中用分层抽样的方法抽取
组中用分层抽样的方法抽取![]() 人,再从这
人,再从这![]() 人中随机抽取
人中随机抽取![]() 人赠送礼品,求抽取的
人赠送礼品,求抽取的![]() 人中至少有
人中至少有![]() 人年龄在第
人年龄在第![]() 组的概率;
组的概率;
(Ⅱ)把年龄在第![]() ,
,![]() ,
,![]() 组的人称为青少年组,年龄在第
组的人称为青少年组,年龄在第![]() ,
,![]() 组的人称为中老年组,若选出的
组的人称为中老年组,若选出的![]() 人中不关注网约车安全问题的人中老年人有
人中不关注网约车安全问题的人中老年人有![]() 人,问是否有
人,问是否有![]() 的把握认为是否关注网约车安全问题与年龄有关?附:
的把握认为是否关注网约车安全问题与年龄有关?附:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
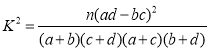 ,
,![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】某工厂加工一批零件,加工过程中会产生次品,根据经验可知,其次品率p与日产量x(万件)之间满足函数关系式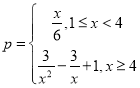 ,已知每生产1万件合格品可获利2万元,但生产1万件次品将亏损1万元(次品率=次品数/生产量)
,已知每生产1万件合格品可获利2万元,但生产1万件次品将亏损1万元(次品率=次品数/生产量)
(1)试写出加工这批零件的日盈利额y(万元)与日产量x(万件)的函数;
(2)当日产量为多少时,可获得最大利润?最大利润为多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com