
科目: 来源: 题型:
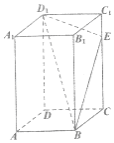
【题目】如图,已知在长方体![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 为
为![]() 上的一个动点,平面
上的一个动点,平面![]() 与棱
与棱![]() 交于点
交于点![]() ,给出下列命题:
,给出下列命题:
①四棱锥![]() 的体积为20;
的体积为20;
②存在唯一的点![]() ,使截面四边形
,使截面四边形![]() 的周长取得最小值
的周长取得最小值![]() ;
;
③当![]() 点不与
点不与![]() ,
,![]() 重合时,在棱
重合时,在棱![]() 上均存在点
上均存在点![]() ,使得
,使得![]() 平面
平面![]() ;
;
④存在唯一的点![]() ,使得
,使得![]() 平面
平面![]() ,且
,且![]() .
.
其中正确的命题是_____(填写所有正确的序号)
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数![]() .
.
(1)若函数![]() 在
在![]() ,
,![]() 上单调递增,求实数
上单调递增,求实数![]() 的取值范围;
的取值范围;
(2)若函数![]() 在
在![]() 处的切线平行于
处的切线平行于![]() 轴,是否存在整数
轴,是否存在整数![]() ,使不等式
,使不等式![]() 在
在![]() 时恒成立?若存在,求出
时恒成立?若存在,求出![]() 的最大值;若不存在,请说明理由.
的最大值;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】某蛋糕店每天制作生日蛋糕若干个,每个生日蛋糕成本为50元,每个蛋糕的售价为100元,如果当天卖不完,剩余的蛋糕作垃圾处理.现搜集并整理了100天生日蛋糕的日需求量(单位:个),得到如图所示的柱状图.100天记录的各需求量的频率作为每天各需求量发生的概率.

(1)若该蛋糕店某一天制作生日蛋糕17个,设当天的需求量为![]() ,则当天的利润
,则当天的利润![]() (单位:元)是多少?
(单位:元)是多少?
(2)若蛋糕店一天制作17个生日蛋糕.
①求当天的利润![]() (单位:元)关于当天需求量
(单位:元)关于当天需求量![]() 的函数解析式;
的函数解析式;
②求当天的利润不低于600圆的概率.
(3)若蛋糕店计划一天制作16个或17个生日蛋糕,请你以蛋糕店一天利润的平均值作为决策依据,应该制作16个还是17个生日蛋糕?
查看答案和解析>>
科目: 来源: 题型:
【题目】椭圆![]() +
+![]() =1(a>b>0)的一个焦点为F1,若椭圆上存在一个点P,满足以椭圆短轴为直径的圆与线段PF1相切于该线段的中点,则椭圆的离心率为________.
=1(a>b>0)的一个焦点为F1,若椭圆上存在一个点P,满足以椭圆短轴为直径的圆与线段PF1相切于该线段的中点,则椭圆的离心率为________.
查看答案和解析>>
科目: 来源: 题型:
【题目】交强险是车主必须为机动车购买的险种,若普通6座以下私家车投保交强险第一年的费用 (基准保费)统一为![]() 元,在下一年续保时,实行的是费率浮动机制,保费是与上一年度车辆发生道路交通安全违法行为或者道路交通事故的情况相联系的.交强险第二年价格计算公式具体如下:交强险最终保费
元,在下一年续保时,实行的是费率浮动机制,保费是与上一年度车辆发生道路交通安全违法行为或者道路交通事故的情况相联系的.交强险第二年价格计算公式具体如下:交强险最终保费![]() 基准保费
基准保费![]() (
(![]() 浮动比率
浮动比率![]() ).发生交通事故的次数越多,出险次数的就越多,费率也就越髙,具体浮动情况如下表:
).发生交通事故的次数越多,出险次数的就越多,费率也就越髙,具体浮动情况如下表:

某机构为了研究某一品牌普通6座以下私家车的投保情况,为此搜集并整理了100辆这一品牌普通6座以下私家车一年内的出险次数,得到下面的柱状图:

已知小明家里有一辆该品牌普通6座以下私家车且需要续保,续保费用为![]() 元.
元.
(1)记![]() 为事件“
为事件“![]() ”,求
”,求![]() 的估计值;
的估计值;
(2)求![]() 的平均估计值.
的平均估计值.
查看答案和解析>>
科目: 来源: 题型:
【题目】为了解某校学生参加社区服务的情况,采用按性别分层抽样的方法进行调查.已知该校共有学生960人,其中男生560人,从全校学生中抽取了容量为n的样本,得到一周参加社区服务时间的统计数据如下:
超过1小时 | 不超过1小时 | |
男 | 20 | 8 |
女 | 12 | m |
(1)求m,n;
(2)能否有95%的把握认为该校学生一周参加社区服务时间是否超过1小时与性别有关?
(3)从该校学生中随机调查60名学生,一周参加社区服务时间超过1小时的人数记为X,以样本中学生参加社区服务时间超过1小时的频率作为该事件发生的概率,求X的分布列和数学期望.
附:
P(K2≥k) | 0.050 | 0.010 | 0.001 |
k | 3.841 | 6.635 | 10.828 |
K2![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知![]() 是圆锥的顶点,
是圆锥的顶点,![]() 是圆锥底面的直径,
是圆锥底面的直径,![]() 是底面圆周上一点,
是底面圆周上一点,![]() ,
,![]() ,平面
,平面![]() 和平面
和平面![]() 将圆锥截去部分后的几何体如图所示.
将圆锥截去部分后的几何体如图所示.
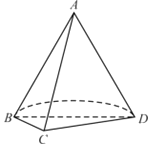
(1)求![]() 与底面所成的角;
与底面所成的角;
(2)求该几何体的体积;
(3)求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com