
科目: 来源: 题型:
【题目】已知抛物线![]() :
:![]() (
(![]() )的焦点为
)的焦点为![]() ,准线为
,准线为![]() ,若点
,若点![]() 在抛物线
在抛物线![]() 上,点
上,点![]() 在直线
在直线![]() 上,且
上,且![]() 是周长为12的等边三角形.
是周长为12的等边三角形.
(1)求抛物线![]() 的标准方程;
的标准方程;
(2)设过点![]() 的直线
的直线![]() 与抛物线
与抛物线![]() 交于不同的两点
交于不同的两点![]() ,
,![]() ,若
,若![]() ,求直线
,求直线![]() 斜率的取值范围.
斜率的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】细叶青萎藤又称海风藤,俗称穿山龙,属木质藤本植物,是我国常用大宗中药材,以根茎入药,具有舒筋活血、祛风止痛、止咳平喘、强身健体等医疗保健功效.通过研究光照、温度和沙藏时间对细叶青萎藤种子萌发的影响,结果表明,细叶青萎藤种子发芽率和发芽指数均随着沙藏时间的延长而提高.
下表给岀了2019年种植的一批试验细叶青萎藤种子6组不同沙藏时间发芽的粒数.经计算:
沙藏时间 | 22 | 23 | 25 | 27 | 29 | 30 |
发芽数 | 8 | 11 | 20 | 30 | 59 | 70 |
![]() ,
,![]() ,
,![]() ,
,![]() .其中
.其中![]() ,
,![]() 分别为试验数据中的天数和发芽粒数,
分别为试验数据中的天数和发芽粒数,![]() .
.
(1)求![]() 关于
关于![]() 的回归方程
的回归方程![]() (
(![]() 和
和![]() 都精确到0.01);
都精确到0.01);
(2)在题中的6组发芽的粒数不大于30的组数中,任意抽岀两组,则这两组数据中至少有一组满足“![]() ”的概率是多少?
”的概率是多少?
附:对于一组数据![]() ,
,![]() ,…,
,…,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为: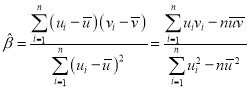 ,
,![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数,将曲线
为参数,将曲线![]() 经过伸缩变换
经过伸缩变换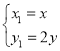 后得到曲线
后得到曲线![]() .在以原点为极点,
.在以原点为极点,![]() 轴正半轴为极轴的极坐标系中,直线
轴正半轴为极轴的极坐标系中,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)说明曲线![]() 是哪一种曲线,并将曲线
是哪一种曲线,并将曲线![]() 的方程化为极坐标方程;
的方程化为极坐标方程;
(2)已知点![]() 是曲线
是曲线![]() 上的任意一点,又直线
上的任意一点,又直线![]() 上有两点
上有两点![]() 和
和![]() ,且
,且![]() ,又点
,又点![]() 的极角为
的极角为![]() ,点
,点![]() 的极角为锐角.求:
的极角为锐角.求:
①点![]() 的极角;
的极角;
②![]() 面积的取值范围.
面积的取值范围.
查看答案和解析>>
科目: 来源: 题型:
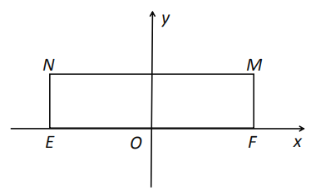
【题目】已知矩形EFMN,![]() ,
,![]() ,以EF的中点O为原点,建立如图的平面直角坐标系,若椭圆
,以EF的中点O为原点,建立如图的平面直角坐标系,若椭圆![]() 以E,F为焦点,且经过M,N两点.
以E,F为焦点,且经过M,N两点.
(1)求椭圆![]() 的方程;
的方程;
(2)直线![]() 与
与![]() 相交于A,B两点,在y轴上是否存在点C,使得△ABC为正三角形,若存在,求出l的方程;若不存在,说明理由.
相交于A,B两点,在y轴上是否存在点C,使得△ABC为正三角形,若存在,求出l的方程;若不存在,说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】美团外卖和百度外卖两家公司其“骑手”的日工资方案如下:美团外卖规定底薪70元,每单抽成1元;百度外卖规定底薪100元,每日前45单无抽成,超出45单的部分每单抽成6元,假设同一公司的“骑手”一日送餐单数相同,现从两家公司个随机抽取一名“骑手”并记录其100天的送餐单数,得到如下条形图:
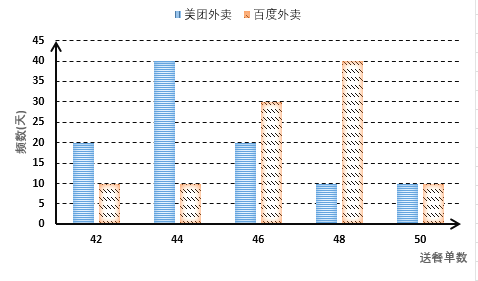
(Ⅰ)求百度外卖公司的“骑手”一日工资![]() (单位:元)与送餐单数
(单位:元)与送餐单数![]() 的函数关系;
的函数关系;
(Ⅱ)若将频率视为概率,回答下列问题:
①记百度外卖的“骑手”日工资为![]() (单位:元),求
(单位:元),求![]() 的分布列和数学期望;
的分布列和数学期望;
②小明拟到这两家公司中的一家应聘“骑手”的工作,如果仅从日收入的角度考虑,请你利用所学的统计学知识为他作出选择,并说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知多面体ABCDEF中,四边形ABFE为正方形,![]() ,
,![]() ,G为AB的中点,
,G为AB的中点,![]() .
.

(1)求证:![]() 平面CDEF;
平面CDEF;
(2)求平面ACD与平面BCF所成锐二面角的余弦值.
查看答案和解析>>
科目: 来源: 题型:
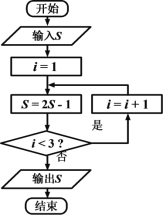
【题目】《算法统宗》是中国古代数学名著,由明代数学家程大位所著,该作完善了珠算口诀,确立了算盘用法,完成了由筹算到珠算的彻底转变,该作中有题为“李白沽酒”“李白街上走,提壶去买酒。遇店加一倍,见花喝一斗,三遇店和花,喝光壶中酒。借问此壶中,原有多少酒?”,如图为该问题的程序框图,若输出的![]() 值为0,则开始输入的
值为0,则开始输入的![]() 值为( )
值为( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com