
科目: 来源: 题型:
【题目】随着网络的发展,网上购物越来越受到人们的喜爱,各大购物网站为增加收入,促销策略越来越多样化,促销费用也不断增加.下表是某购物网站2017年1-8月促销费用(万元)和产品销量(万件)的具体数据.

(1)根据数据绘制的散点图能够看出可用线性回归模型拟合![]() 与
与![]() 的关系,请用相关系数
的关系,请用相关系数![]() 加以说明;(系数精确到0.001)
加以说明;(系数精确到0.001)
(2)建立![]() 关于
关于![]() 的回归方程
的回归方程![]() (系数精确到0.01);如果该公司计划在9月份实现产品销量超6万件,预测至少需投入促销费用多少万元(结果精确到0.01).
(系数精确到0.01);如果该公司计划在9月份实现产品销量超6万件,预测至少需投入促销费用多少万元(结果精确到0.01).
参考数据: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,其中
,其中![]() ,
, ![]() 分别为第
分别为第![]() 个月的促销费用和产品销量,
个月的促销费用和产品销量, ![]() .
.
参考公式:(1)样本![]() 的相关系数
的相关系数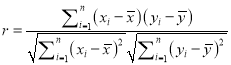
(2)对于一组数据![]() ,
, ![]() ,
, ![]() ,
, ![]() ,其回归方程
,其回归方程![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为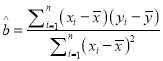 ,
, ![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】拉丁舞,又称拉丁风情舞或自由社交舞,它是拉丁人民在漫长的历史长河中形成的,包含伦巴、恰恰、牛仔舞、桑巴、斗牛舞、深受人民的喜爱.某艺术培训机构为了调查本校学院对拉丁舞的学习情况,分别在刚学习了一个季度的本校大班(8岁以下)及种子班(8岁以上)的学员中各随机抽取了15名学员进行摸底考试,这30名学员考试成绩的茎叶图如图所示.

规定:成绩不低于85分,则认为成绩优秀;成绩低于85分,则认为成绩一般.
(1)根据上述数据填写下列2×2联表:
成绩优秀 | 成绩一般 | 总计 | |
大班 | |||
种子班 | |||
总计 |
判断是否有95%的把握认为成绩优秀或成绩一般与学员的年龄有关;
(2)在大班及种子班的参加摸底考试且成绩优秀的学员中以分层抽样的方式抽取6名学员进行特别集训,集训后,再对这6名学员进行测试,按测试成绩,取前3名授予“舞蹈小精灵”称号,在被授予“舞蹈小精灵”称号的学员中,求种子班的学员恰好有2人的概率.
参考公式及数据: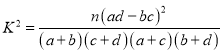 ,
,![]() .
.
| 0.100 | 0.050 | 0.025 | 0.010 |
| 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目: 来源: 题型:
【题目】2019年,中华人民共和国成立70周年,为了庆祝建国70周年,某中学在全校进行了一次爱国主义知识竞赛,共1000名学生参加,答对题数(共60题)分布如下表所示:
组别 |
|
|
|
|
|
|
频数 | 10 | 185 | 265 | 400 | 115 | 25 |
答对题数![]() 近似服从正态分布
近似服从正态分布![]() ,
,![]() 为这1000人答对题数的平均值(同一组数据用该组区间的中点值作为代表).
为这1000人答对题数的平均值(同一组数据用该组区间的中点值作为代表).
(1)估计答对题数在![]() 内的人数(精确到整数位).
内的人数(精确到整数位).
(2)学校为此次参加竞赛的学生制定如下奖励方案:每名同学可以获得2次抽奖机会,每次抽奖所得奖品的价值与对应的概率如下表所示.
获得奖品的价值(单位:元) | 0 | 10 | 20 |
概率 |
|
|
|
用![]() (单位:元)表示学生甲参与抽奖所得奖品的价值,求
(单位:元)表示学生甲参与抽奖所得奖品的价值,求![]() 的分布列及数学期望.
的分布列及数学期望.
附:若![]() ,则
,则![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知向量
中,已知向量![]() ,
,![]() ,且
,且![]() .记动点
.记动点![]() 的轨迹为
的轨迹为![]() .
.
(1)求![]() 的方程;
的方程;
(2)已知直线![]() 过坐标原点,且与(1)中的轨迹
过坐标原点,且与(1)中的轨迹![]() 交于
交于![]() 两点,
两点,![]() 在第三象限,且
在第三象限,且![]() 轴,垂足为
轴,垂足为![]() ,连接
,连接![]() 并延长交
并延长交![]() 于点
于点![]() ,求
,求![]() 的面积的最大值.
的面积的最大值.
查看答案和解析>>
科目: 来源: 题型:
【题目】在直角坐标系![]() 中,已知直线
中,已知直线![]() 的直角坐标方程为
的直角坐标方程为![]() ,曲线
,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以直角坐标系原点为极点,
为参数),以直角坐标系原点为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 和直线
和直线![]() 的极坐标方程;
的极坐标方程;
(2)已知直线![]() 与曲线
与曲线![]() 、
、![]() 相交于异于极点的点
相交于异于极点的点![]() ,若
,若![]() 的极径分别为
的极径分别为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,O为坐标原点,点F为抛物线C1:![]() 的焦点,且抛物线C1上点P处的切线与圆C2:
的焦点,且抛物线C1上点P处的切线与圆C2:![]() 相切于点Q.
相切于点Q.

(Ⅰ)当直线PQ的方程为![]() 时,求 抛物线C1的方程;
时,求 抛物线C1的方程;
(Ⅱ)当正数P变化时,记S1 ,S2分别为△FPQ,△FOQ的面积,求![]() 的最小值.
的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com