
科目: 来源: 题型:
【题目】为了保障某治疗新冠肺炎药品的主要药理成分在国家药品监督管理局规定的值范围内,武汉某制药厂在该药品的生产过程中,检验员在一天中按照规定从该药品生产线上随机抽取20件产品进行检测,测量其主要药理成分含量(单位:mg).根据生产经验,可以认为这条药品生产线正常状态下生产的产品的主要药理成分含量服从正态分布N(μ,σ2).在一天内抽取的20件产品中,如果有一件出现了主要药理成分含量在(μ﹣3σ,μ+3σ)之外的药品,就认为这条生产线在这一天的生产过程可能出现了异常情况,需对本次的生产过程进行检查.
(1)下面是检验员在2月24日抽取的20件药品的主要药理成分含量:
10.02 | 9.78 | 10.04 | 9.92 | 10.14 | 10.04 | 9.22 | 10.13 | 9.91 | 9.95 |
10.09 | 9.96 | 9.88 | 10.01 | 9.98 | 9.95 | 10.05 | 10.05 | 9.96 | 10.12 |
经计算得![]() xi=9.96,s
xi=9.96,s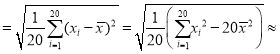 0.19;其中xi为抽取的第i件药品的主要药理成分含量,i=1,2,…,20.用样本平均数
0.19;其中xi为抽取的第i件药品的主要药理成分含量,i=1,2,…,20.用样本平均数![]() 作为μ的估计值
作为μ的估计值![]() ,用样本标准差s作为σ的估计值
,用样本标准差s作为σ的估计值![]() ,利用估计值判断是否需对本次的生产过程进行检查?
,利用估计值判断是否需对本次的生产过程进行检查?
(2)假设生产状态正常,记X表示某天抽取的20件产品中其主要药理成分含量在(μ﹣3σ,μ+3σ)之外的药品件数,求/span>P(X=1)及X的数学期望.
附:若随机变量Z服从正态分布N(μ,σ2),则P(μ﹣3σ<Z<μ+3σ)≈0.9974,0.997419≈0.95.
查看答案和解析>>
科目: 来源: 题型:
【题目】函数f(x)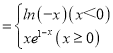 ,若关于x的方程f2(x)﹣af(x)+a﹣a2=0有四个不等的实数根,则a的取值范围是( )
,若关于x的方程f2(x)﹣af(x)+a﹣a2=0有四个不等的实数根,则a的取值范围是( )
A.![]() B.(﹣∞,﹣1)∪[1,+∞)
B.(﹣∞,﹣1)∪[1,+∞)
C.(﹣∞,﹣1)∪{1}D.(﹣1,0)∪{1}
查看答案和解析>>
科目: 来源: 题型:
【题目】我国古代有着辉煌的数学研究成果,其中《周髀算经》、《九章算术》、《海岛算经》、《孙子算经》、《缉古算经》有着丰富多彩的内容,是了解我国古代数学的重要文献.这5部专著中有3部产生于汉、魏、晋、南北朝时期.现拟从这5部专著中选择2部作为学生课外兴趣拓展参考书目,则所选2部专著中至少有一部不是汉、魏、晋、南北朝时期专著的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数f(x)=x-lnx,g(x)=x2-ax.
(1)求函数f(x)在区间[t,t+1](t>0)上的最小值m(t);
(2)令h(x)=g(x)-f(x),A(x1,h(x1)),B(x2,h(x2))(x1≠x2)是函数h(x)图像上任意两点,且满足![]() >1,求实数a的取值范围;
>1,求实数a的取值范围;
(3)若x∈(0,1],使f(x)≥![]() 成立,求实数a的最大值.
成立,求实数a的最大值.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆![]() 的焦点为
的焦点为![]() ,
,![]() ,离心率为
,离心率为![]() ,点P为椭圆C上一动点,且
,点P为椭圆C上一动点,且![]() 的面积最大值为
的面积最大值为![]() ,O为坐标原点.
,O为坐标原点.
(1)求椭圆C的方程;
(2)设点![]() ,
,![]() 为椭圆C上的两个动点,当
为椭圆C上的两个动点,当![]() 为多少时,点O到直线MN的距离为定值.
为多少时,点O到直线MN的距离为定值.
查看答案和解析>>
科目: 来源: 题型:
【题目】某种大型医疗检查机器生产商,对一次性购买2台机器的客户,推出两种超过质保期后两年内的延保维修优惠方案:方案一:交纳延保金7000元,在延保的两年内可免费维修2次,超过2次每次收取维修费2000元;方案二:交纳延保金10000元,在延保的两年内可免费维修4次,超过4次每次收取维修费1000元.某医院准备一次性购买2台这种机器。现需决策在购买机器时应购买哪种延保方案,为此搜集并整理了50台这种机器超过质保期后延保两年内维修的次数,得下表:
维修次数 | 0 | 1 | 2 | 3 |
台数 | 5 | 10 | 20 | 15 |
以这50台机器维修次数的频率代替1台机器维修次数发生的概率,记X表示这2台机器超过质保期后延保的两年内共需维修的次数。
(1)求X的分布列;
(2)以所需延保金及维修费用的期望值为决策依据,医院选择哪种延保方案更合算?
查看答案和解析>>
科目: 来源: 题型:
【题目】已知双曲线![]() :
:![]() 的右焦点为
的右焦点为![]() ,半焦距
,半焦距![]() ,点
,点![]() 到右准线
到右准线![]() 的距离为
的距离为![]() ,过点
,过点![]() 作双曲线
作双曲线![]() 的两条互相垂直的弦
的两条互相垂直的弦![]() ,
,![]() ,设
,设![]() ,
,![]() 的中点分别为
的中点分别为![]() ,
,![]() .
.
(1)求双曲线![]() 的标准方程;
的标准方程;
(2)证明:直线![]() 必过定点,并求出此定点坐标.
必过定点,并求出此定点坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知![]() ,
,![]() 分别是
分别是![]() 的边
的边![]() ,
,![]() 上的一点,
上的一点,![]() ,将
,将![]() 沿
沿![]() 折起为
折起为![]() ,使
,使![]() 点位于
点位于![]() 点的位置,连接
点的位置,连接![]() ,
,![]() ,
,![]() .
.
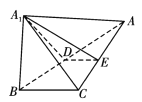
(1)若![]() ,
,![]() 分别是
分别是![]() ,
,![]() 的中点,平面
的中点,平面![]() 与平面
与平面![]() 的交线为
的交线为![]() ,证明:
,证明:![]() ;
;
(2)若平面![]() 平面
平面![]() ,
,![]() 与
与![]() 的面积分别为4和9,
的面积分别为4和9,![]() ,求三棱锥
,求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com