
科目: 来源: 题型:
【题目】公元五世纪,数学家祖冲之估计圆周率![]() 的值的范围是:3.1415926<
的值的范围是:3.1415926<![]() <3.1415927,为纪念祖冲之在圆周率的成就,把3.1415926称为“祖率”,这是中国数学的伟大成就.某小学教师为帮助同学们了解“祖率”,让同学们把小数点后的7位数字1,4,1,5,9,2,6进行随机排列,整数部分3不变,那么可以得到大于3.14的不同数字有( )
<3.1415927,为纪念祖冲之在圆周率的成就,把3.1415926称为“祖率”,这是中国数学的伟大成就.某小学教师为帮助同学们了解“祖率”,让同学们把小数点后的7位数字1,4,1,5,9,2,6进行随机排列,整数部分3不变,那么可以得到大于3.14的不同数字有( )
A.2280B.2120C.1440D.720
查看答案和解析>>
科目: 来源: 题型:
【题目】2018年11月5日至10日,首届中国国际进口博览会在国家会展中心(上海)举行,吸引了58个“一带一路”沿线国家的超过1000多家企业参展,成为共建“一带一路”的又一个重要支撑.某企业为了参加这次盛会,提升行业竞争力,加大了科技投入.该企业连续6年来的科技投入![]() (百万元)与收益
(百万元)与收益![]() (百万元)的数据统计如下:
(百万元)的数据统计如下:
科技投入 | 2 | 4 | 6 | 8 | 10 | 12 |
收益 | 5.6 | 6.5 | 12.0 | 27.5 | 80.0 | 129.2 |
并根据数据绘制散点图如图所示:
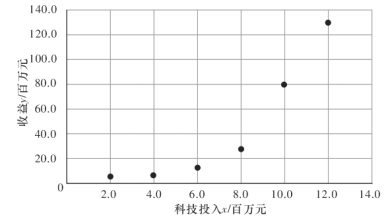
根据散点图的特点,甲认为样本点分布在指数曲线![]() 的周围,据此他对数据进行了一些初步处理.如下表:
的周围,据此他对数据进行了一些初步处理.如下表:
|
|
|
|
|
|
43.5 | 4.5 | 854.0 | 34.7 | 12730.4 | 70 |
其中![]() ,
,![]() .
.
(1)(i)请根据表中数据,建立![]() 关于
关于![]() 的回归方程(保留一位小数);
的回归方程(保留一位小数);
(ii)根据所建立的回归方程,若该企业想在下一年收益达到2亿,则科技投入的费用至少要多少?(其中![]() )
)
(2)乙认为样本点分布在二次曲线![]() 的周围,并计算得回归方程为
的周围,并计算得回归方程为![]() ,以及该回归模型的相关指数
,以及该回归模型的相关指数![]() ,试比较甲乙两人所建立的模型,谁的拟合效果更好.
,试比较甲乙两人所建立的模型,谁的拟合效果更好.
附:对于一组数据![]() ,
,![]() ,…,
,…,![]() ,其回归直线方程
,其回归直线方程![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为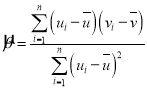 ,
,![]() ,相关指数:
,相关指数: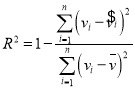 .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知动圆![]() 与
与![]() 轴相切,且与圆
轴相切,且与圆![]() :
:![]() 外切;
外切;
(1)求动圆圆心![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)若直线![]() 过定点
过定点![]() ,且与轨迹
,且与轨迹![]() 交于
交于![]() 、
、![]() 两点,与圆
两点,与圆![]() 交于
交于![]() 、
、![]() 两点,若点
两点,若点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,求
,求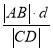 的最小值.
的最小值.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知F1、F2是椭圆![]() 的左、右焦点,A是椭圆上位于第一象限内的一点,点B也在椭圆上,且满足
的左、右焦点,A是椭圆上位于第一象限内的一点,点B也在椭圆上,且满足![]() (O是坐标原点),
(O是坐标原点),![]() 若椭圆的离心率等于
若椭圆的离心率等于![]()
(1)求直线AB的方程;
(2)若三角形ABF2的面积等于![]() ,求椭圆的方程.
,求椭圆的方程.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数f(x)既是二次函数又是幂函数,函数g(x)是R上的奇函数,函数![]() =
=![]() +1,则h(2018)+h(2017)+h(2016)+…+h(1)+h(0)+h(﹣1)+…h(﹣2016)+h(﹣2017)+h(﹣2018)=___________
+1,则h(2018)+h(2017)+h(2016)+…+h(1)+h(0)+h(﹣1)+…h(﹣2016)+h(﹣2017)+h(﹣2018)=___________
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com