
科目: 来源: 题型:
【题目】为增强学生法治观念,营造“学宪法、知宪法、守宪法”的良好校园氛围,某学校开展了“宪法小卫士”活动,并组织全校学生进行法律知识竞赛.现从全校学生中随机抽取50人,统计他们的竞赛成绩,并得到如表所示的频数分布表.
分数段 |
|
|
|
|
|
人数 | 5 | 15 | 15 | 12 |
|
(Ⅰ)求频数分布表中的![]() 的值,并估计这50名学生竞赛成绩的中位数(精确到0.1);
的值,并估计这50名学生竞赛成绩的中位数(精确到0.1);
(Ⅱ)将成绩在![]() 内定义为“合格”,成绩在
内定义为“合格”,成绩在![]() 内定义为“不合格”.请将列联表补充完整.
内定义为“不合格”.请将列联表补充完整.
合格 | 不合格 | 合计 | |
高一新生 | 12 | ||
非高一新生 | 6 | ||
合计 |
试问:是否有95%的把握认为“法律知识的掌握合格情况”与“是否是高一新生”有关?说明你的理由;
(Ⅲ)在(Ⅱ)的前提下,在该50人中,按“合格与否”进行分层抽样,随机抽取5人,再从这5人中随机抽取2人,求恰好2人都合格的概率.
附:
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
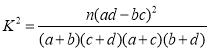 ,
,![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】“二进制”来源于我国古代的《易经》,该书中有两类最基本的符号:“—”和“——”,其中“—”在二进制中记作“1”,“——”在二进制中记作“0”,例如二进制数![]() 化为十进制的计算如下:
化为十进制的计算如下:![]() .若从两类符号中任取2个符号进行排列,则得到的二进制数所对应的十进制数大于2的概率为( )
.若从两类符号中任取2个符号进行排列,则得到的二进制数所对应的十进制数大于2的概率为( )
A.0B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】近几年,在国家大力支持和引导下,中国遥感卫星在社会生产和生活各领域的应用范围不断扩大,中国人民用遥感卫星系统研制工作取得了显著成绩,逐步形成了气象、海洋、陆地资源和科学试验等遥感卫星系统.如图是2007—2018年中国卫星导航与位置服务产业总体产值规模(万亿)及增速(%)的统计图,则下列结论中错误的是( )
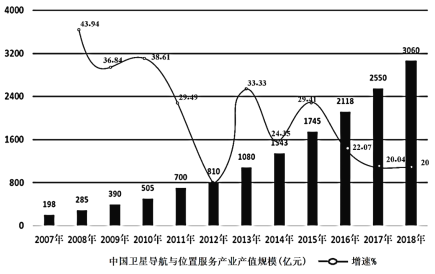
A.2017年中国卫星导航与位置服务产业总体产值规模达到2550亿元,较2016年增长20.40%
B.若2019年中国卫星导航与位置服务产业总体产值规模保持2018年的增速,总体产值规模将达3672亿元
C.2007—2018年中国卫星导航与位置服务产业总体产值规模逐年增加,但不与时间成正相关
D.2007—2018年中国卫星导航与位置服务产业总体产值规模的增速中有些与时间成负相关
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆![]() :
:![]() (
(![]() )的离心率为
)的离心率为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,且椭圆
,且椭圆![]() 上任意一点到
上任意一点到![]() 点的最大距离为
点的最大距离为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() ,
,![]() 两点,点
两点,点![]() 为椭圆
为椭圆![]() 长轴上的一点,求
长轴上的一点,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目: 来源: 题型:
【题目】某市正在进行创建全国文明城市的复验工作,为了解市民对“创建全国文明城市”的知识知晓程度,某权威调查机构对市民进行随机调查,并对调查结果进行统计,共分为优秀和一般两类,先从结果中随机抽取100份,统计得出如下![]() 列联表:
列联表:
优秀 | 一般 | 总计 | |
男 | 25 | 25 | 50 |
女 | 30 | 20 | 50 |
总计 | 55 | 45 | 100 |
(1)根据上述列联表,是否有![]() 的把握认为“创城知识的知晓程度是否为优秀与性别有关”?
的把握认为“创城知识的知晓程度是否为优秀与性别有关”?
(2)现从调查结果为一般的市民中,按分层抽样的方法从中抽取9人,然后再从这9人中随机抽取3人,求这三位市民中男女都有的概率;
(3)以样本估计总体,视样本频率为概率,从全市市民中随机抽取10人,用![]() 表示这10人中优秀的人数,求随机变量
表示这10人中优秀的人数,求随机变量![]() 的期望和方差.
的期望和方差.
附:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
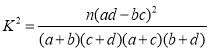 (其中
(其中![]() ).
).
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为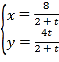 (
(![]() 为参数).以坐标原点
为参数).以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若射线![]() (
(![]() )与直线
)与直线![]() 和曲线
和曲线![]() 分别交于
分别交于![]() ,
,![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com