
科目: 来源: 题型:
【题目】我市某区2018年房地产价格因“棚户区改造”实行货币化补偿,使房价快速走高,为抑制房价过快上涨,政府从2019年2月开始采用实物补偿方式(以房换房),3月份开始房价得到很好的抑制,房价渐渐回落,以下是2019年2月后该区新建住宅销售均价的数据:
月份 | 3 | 4 | 5 | 6 | 7 |
价格 | 83 | 82 | 80 | 78 | 77 |
(1)研究发现,3月至7月的各月均价![]() (百元/平方米)与月份
(百元/平方米)与月份![]() 之间具有较强的线性相关关系,求价格
之间具有较强的线性相关关系,求价格![]() (百元/平方米)关于月份
(百元/平方米)关于月份![]() 的线性回归方程;
的线性回归方程;
(2)用![]() 表示用(1)中所求的线性回归方程得到的与
表示用(1)中所求的线性回归方程得到的与![]() 对应的销售均价的估计值,3月份至7月份销售均价估计值
对应的销售均价的估计值,3月份至7月份销售均价估计值![]() 与实际相应月份销售均价
与实际相应月份销售均价![]() 差的绝对值记为
差的绝对值记为![]() ,即
,即![]() ,
,![]() .若
.若![]() ,则将销售均价的数据
,则将销售均价的数据称为一个“好数据”,现从5个销售均价数据中任取2个,求抽取的2个数据均是“好数据”的概率.
参考公式:回归方程系数公式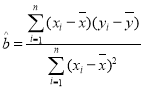 ,
,![]() ;参考数据:
;参考数据:![]() ,
,![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线l的参数方程是
中,直线l的参数方程是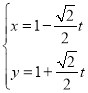 (t为参数),以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程是
(t为参数),以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程是![]() .
.
(1)证明:直线l与曲线C相切;
(2)设直线l与x轴、y轴分别交于点A,B,点P是曲线C上任意一点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】新疆小南瓜以沙甜闻名全国,小田计划从新疆运输小南瓜去上海,随机从某瓜农的瓜地里挑选了100个,其质量分别在![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() (单位:克)中,经统计得频率分布直方图如图所示,将频率视为概率.
(单位:克)中,经统计得频率分布直方图如图所示,将频率视为概率.
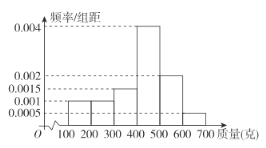
(1)请根据频率分布直方图估计该瓜农的小南瓜的平均质量;
(2)已知瓜地里还有2万个小南瓜已经成熟,可以采摘,小田想全部购买,可是瓜农要求超过400克的小南瓜以5元一个的价格出售,其他的以3元一个的价格出售.将频率视为概率,若新疆到上海往返的运费约2000元,请问这2万个小南瓜在上海以每斤(500克)多少元定价才能保证小田的利润不少于5000元?(结果保留一位小数)
(3)某天王阿姨在上海某超市的蔬菜柜台上看到小田从新疆采摘的新疆小南瓜,已知柜台上有若干个,若质量超过500克的小南瓜为“优质品”,王阿姨随机购买了20个小南瓜,求王阿姨购买的小南瓜中“优质品”个数的期望.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆C:![]() (
(![]() )的左,右焦点为
)的左,右焦点为![]() ,
,![]() ,且焦距为
,且焦距为![]() ,点
,点![]() ,
,![]() 分别为椭圆C的上、下顶点,满足
分别为椭圆C的上、下顶点,满足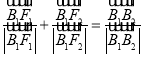 .
.
(1)求椭圆C的方程;
(2)已知点![]() ,椭圆C上的两个动点M,N满足
,椭圆C上的两个动点M,N满足![]() ,求证:直线
,求证:直线![]() 过定点.
过定点.
查看答案和解析>>
科目: 来源: 题型:
【题目】支付宝和微信支付已经成为现如今最流行的电子支付方式,某市通过随机询问100名居民(男女居民各50名)喜欢支付宝支付还是微信支付,得到如下的![]() 列联表:
列联表:
支付宝支付 | 微信支付 | |
男 | 40 | 10 |
女 | 25 | 25 |
附表及公式: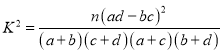 ,
,![]() .
.
P( | 0.050 | 0.010 | 0.001 |
k | 3.841 | 6.635 | 10.828 |
则下面结论正确的是( )
A.有![]() 以上的把握认为“支付方式与性别有关”
以上的把握认为“支付方式与性别有关”
B.在犯错误的概率超过![]() 的前提下,认为“支付方式与性别有关”
的前提下,认为“支付方式与性别有关”
C.在犯错误的概率不超过![]() 的前提下,认为“支付方式与性别有关”
的前提下,认为“支付方式与性别有关”
D.有![]() 以上的把握认为“支付方式与性别无关”
以上的把握认为“支付方式与性别无关”
查看答案和解析>>
科目: 来源: 题型:
【题目】在“互联网+”时代的今天,移动互联快速发展,智能手机(Smartphone)技术不断成熟,尤其在5G领域,华为更以![]() 件专利数排名世界第一,打破了以往由美、英、日垄断的前三位置,再次荣耀世界,而华为的价格却不断下降,远低于苹果;智能手机成为了生活中必不可少的工具,学生是对新事物和新潮流反应最快的一个群体之一,越来越多的学生在学校里使用手机,为了解手机在学生中的使用情况,对某学校高二年级
件专利数排名世界第一,打破了以往由美、英、日垄断的前三位置,再次荣耀世界,而华为的价格却不断下降,远低于苹果;智能手机成为了生活中必不可少的工具,学生是对新事物和新潮流反应最快的一个群体之一,越来越多的学生在学校里使用手机,为了解手机在学生中的使用情况,对某学校高二年级![]() 名同学使用手机的情况进行调查,针对调查中获得的“每天平均使用手机进行娱乐活动的时间”进行分组整理得到如下的数据:
名同学使用手机的情况进行调查,针对调查中获得的“每天平均使用手机进行娱乐活动的时间”进行分组整理得到如下的数据:
使用时间(小时) | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
所占比例 | 4% | 10% | 31% | 16% |
| 12% | 2% |
(1)求表中![]() 的值;
的值;
(2)从该学校随机选取一名同学,能否根据题目中所给信息估计出这名学生每天平均使用手机进行娱乐活动小于![]() 小时的概率?若能,请算出这个概率;若不能,请说明理由;
小时的概率?若能,请算出这个概率;若不能,请说明理由;
(3)若从使用手机![]() 小时和
小时和![]() 小时的两组中任取两人,调查问卷,看看他们对使用手机进行娱乐活动的看法,求这
小时的两组中任取两人,调查问卷,看看他们对使用手机进行娱乐活动的看法,求这![]() 人都使用
人都使用![]() 小时的概率.
小时的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数f(x)=|2x﹣a|+|x﹣a+1|.
(1)当a=4时,求解不等式f(x)≥8;
(2)已知关于x的不等式f(x)![]() 在R上恒成立,求参数a的取值范围.
在R上恒成立,求参数a的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】在直角坐标系xOy中,曲线C1的参数方程为![]() (
(![]() 为参数),以坐标原点O为极点,x轴正半轴为极轴建立极坐标系,曲线C2:ρ2﹣4ρcosθ+3=0.
为参数),以坐标原点O为极点,x轴正半轴为极轴建立极坐标系,曲线C2:ρ2﹣4ρcosθ+3=0.
(1)求曲线C1的一般方程和曲线C2的直角坐标方程;
(2)若点P在曲线C1上,点Q曲线C2上,求|PQ|的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com