
科目: 来源: 题型:
【题目】(某工厂生产零件A,工人甲生产一件零件A,是一等品、二等品、三等品的概率分别为![]() ,工人乙生产一件零件A,是一等品、二等品、三等品的概率分别为
,工人乙生产一件零件A,是一等品、二等品、三等品的概率分别为![]() .己知生产一件一等品、二等品、三等品零件A给工厂带来的效益分别为10元、5元、2元.
.己知生产一件一等品、二等品、三等品零件A给工厂带来的效益分别为10元、5元、2元.
(1)试根据生产一件零件A给工厂带来的效益的期望值判断甲乙技术的好坏;
(2)为鼓励工人提高技术,工厂进行技术大赛,最后甲乙两人进入了决赛.决赛规则是:每一轮比赛,甲乙各生产一件零件A,如果一方生产的零件A品级优干另一方生产的零件,则该方得分1分,另一方得分-1分,如果两人生产的零件A品级一样,则两方都不得分,当一方总分为4分时,比赛结束,该方获胜.Pi+4(i=![]() 4,
4,![]() 3,
3,![]() 2,…,4)表示甲总分为i时,最终甲获胜的概率.
2,…,4)表示甲总分为i时,最终甲获胜的概率.
①写出P0,P8的值;
②求决赛甲获胜的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】己知圆F1:(x+1)2 +y2= r2(1≤r≤3),圆F2:(x-1)2+y2= (4-r)2.
(1)证明:圆F1与圆F2有公共点,并求公共点的轨迹E的方程;
(2)已知点Q(m,0)(m<0),过点E斜率为k(k≠0)的直线与(Ⅰ)中轨迹E相交于M,N两点,记直线QM的斜率为k1,直线QN的斜率为k2,是否存在实数m使得k(k1+k2)为定值?若存在,求出m的值,若不存在,说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】在直角坐标系xOy中,以坐标原点为极点,x轴的非负半轴为极轴建立极坐标系;曲线C1的普通方程为(x-1)2 +y2 =1,曲线C2的参数方程为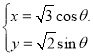 (θ为参数).
(θ为参数).
(Ⅰ)求曲线C1和C2的极坐标方程:
(Ⅱ)设射线θ=![]() (ρ>0)分别与曲线C1和C2相交于A,B两点,求|AB|的值.
(ρ>0)分别与曲线C1和C2相交于A,B两点,求|AB|的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数f(x)=ex-x2 -kx(其中e为自然对数的底,k为常数)有一个极大值点和一个极小值点.
(1)求实数k的取值范围;
(2)证明:f(x)的极大值不小于1.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,三棱柱ABC-A1B1C1中,侧面BCC1B1是菱形,AC=BC=2,∠CBB1=![]() ,点A在平面BCC1B1上的投影为棱BB1的中点E.
,点A在平面BCC1B1上的投影为棱BB1的中点E.
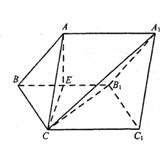
(1)求证:四边形ACC1A1为矩形;
(2)求二面角E-B1C-A1的平面角的余弦值.
查看答案和解析>>
科目: 来源: 题型:
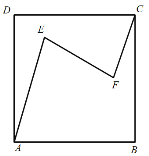
【题目】台球是一项国际上广泛流行的高雅室内体育运动,也叫桌球(中国粤港澳地区的叫法)、撞球(中国台湾地区的叫法)控制撞球点、球的旋转等控制母球走位是击球的一项重要技术,一次台球技术表演节目中,在台球桌上,画出如图正方形ABCD,在点E,F处各放一个目标球,表演者先将母球放在点A处,通过击打母球,使其依次撞击点E,F处的目标球,最后停在点C处,若AE=50cm.EF=40cm.FC=30cm,∠AEF=∠CFE=60°,则该正方形的边长为( )
A.50![]() cmB.40
cmB.40![]() cmC.50cmD.20
cmC.50cmD.20![]() cm
cm
查看答案和解析>>
科目: 来源: 题型:
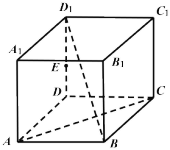
【题目】如图,点E是正方体ABCD-A1B1C1D1的棱DD1的中点,点F,M分别在线段AC,BD1(不包含端点)上运动,则( )
A.在点F的运动过程中,存在EF//BC1
B.在点M的运动过程中,不存在B1M⊥AE
C.四面体EMAC的体积为定值
D.四面体FA1C1B的体积不为定值
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在四棱锥![]() 中,
中,![]() 平面
平面![]() ,四边形
,四边形![]() 为正方形,点
为正方形,点![]() 为线段
为线段![]() 上的点,过
上的点,过![]() 三点的平面与
三点的平面与![]() 交于点
交于点![]() .将①
.将①![]() ,②
,②![]() ,③
,③![]() 中的两个补充到已知条件中,解答下列问题:
中的两个补充到已知条件中,解答下列问题:
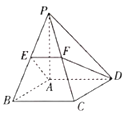
(1)求平面![]() 将四棱锥分成两部分的体积比;
将四棱锥分成两部分的体积比;
(2)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com