
科目: 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),直线
为参数),直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为常数且
为常数且![]() ,
,![]() 为参数).
为参数).
(1)求![]() 和
和![]() 的直角坐标方程;
的直角坐标方程;
(2)若![]() 和
和![]() 相交于
相交于![]() 、
、![]() 两点,以线段
两点,以线段![]() 为一条边作
为一条边作![]() 的内接矩形
的内接矩形![]() ,当矩形
,当矩形![]() 的面积取最大值时,求
的面积取最大值时,求![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】随着智能手机的普及,手机计步软件迅速流行开来,这类软件能自动记载每日健步走的步数,从而为科学健身提供了一定帮助.某企业为了解员工每日健步走的情况,从该企业正常上班的员工中随机抽取300名,统计他们的每日健步走的步数(均不低于4千步,不超过20千步).按步数分组,得到频率分布直方图如图所示.
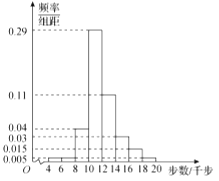
(1)求这300名员工日行步数![]() (单位:千步)的样本平均数(每组数据以该组区间的中点值为代表,结果保留整数);
(单位:千步)的样本平均数(每组数据以该组区间的中点值为代表,结果保留整数);
(2)由直方图可以认为该企业员工的日行步数![]() (单位:千步)服从正态分布
(单位:千步)服从正态分布![]() ,其中
,其中![]() 为样本平均数,标准差
为样本平均数,标准差![]() 的近似值为2,求该企业被抽取的300名员工中日行步数
的近似值为2,求该企业被抽取的300名员工中日行步数![]() 的人数;
的人数;
(3)用样本估计总体,将频率视为概率.若工会从该企业员工中随机抽取2人作为“日行万步”活动的慰问奖励对象,规定:日行步数不超过8千步者为“不健康生活方式者”,给予精神鼓励,奖励金额为每人0元;日行步数为8~14千步者为“一般生活方式者”,奖励金额为每人100元;日行步数为14千步以上者为“超健康生活方式者”,奖励金额为每人200元.求工会慰问奖励金额![]() (单位:元)的分布列和数学期望.
(单位:元)的分布列和数学期望.
附:若随机变量![]() 服从正态分布
服从正态分布![]() ,则
,则![]() ,
,![]()
![]() ,
,![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】1970年4月24日,我国发射了自己的第一颗人造地球卫星“东方红一号”,从此我国开启了人造卫星的新篇章,人造地球卫星绕地球运行遵循开普勒行星运动定律:卫星在以地球为焦点的椭圆轨道上绕地球运行时,其运行速度是变化的,速度的变化服从面积守恒规律,即卫星的向径(卫星与地球的连线)在相同的时间内扫过的面积相等.设椭圆的长轴长、焦距分别为![]() ,
,![]() ,下列结论不正确的是( )
,下列结论不正确的是( )
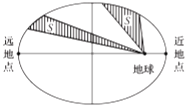
A.卫星向径的最小值为![]()
B.卫星向径的最大值为![]()
C.卫星向径的最小值与最大值的比值越小,椭圆轨道越扁
D.卫星运行速度在近地点时最小,在远地点时最大
查看答案和解析>>
科目: 来源: 题型:
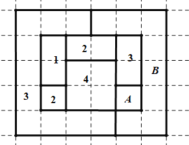
【题目】如图,网格纸上小正方形的边长为1,粗实线围成的各区域上分别且只能标记数字1,2,3,4,相邻区域标记的数字不同,其中,区域![]() 和区域
和区域![]() 标记的数字丢失.若在图上随机取一点,则该点恰好取自标记为1的区域的概率所有可能值中,最大的是( )
标记的数字丢失.若在图上随机取一点,则该点恰好取自标记为1的区域的概率所有可能值中,最大的是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】虚拟现实(![]() )技术被认为是经济发展的新增长点,某地区引进
)技术被认为是经济发展的新增长点,某地区引进![]() 技术后,
技术后,![]() 市场收入(包含软件收入和硬件收入)逐年翻一番,据统计该地区
市场收入(包含软件收入和硬件收入)逐年翻一番,据统计该地区![]() 市场收入情况如图所示,则下列说法错误的是( )
市场收入情况如图所示,则下列说法错误的是( )
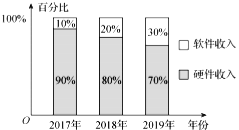
A.该地区2019年的![]() 市场总收入是2017年的4倍
市场总收入是2017年的4倍
B.该地区2019年的![]() 硬件收入比2017年和2018年的硬件收入总和还要多
硬件收入比2017年和2018年的硬件收入总和还要多
C.该地区2019年的![]() 软件收入是2018年的软件收入的3倍
软件收入是2018年的软件收入的3倍
D.该地区2019年的![]() 软件收入是2017年的软件收入的6倍
软件收入是2017年的软件收入的6倍
查看答案和解析>>
科目: 来源: 题型:
【题目】已知抛物线![]() 的焦点为F,点P为抛物线C上一点,
的焦点为F,点P为抛物线C上一点,![]() ,O为坐标原点,
,O为坐标原点,![]() .
.
(1)求抛物线C的方程;
(2)设Q为抛物线C的准线上一点,过点F且垂直于OQ的直线交抛物线C于A,B两点记![]() ,
,![]() 的面积分别为
的面积分别为![]()
![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】2019年上半年我国多个省市暴发了“非洲猪瘟”疫情,生猪大量病死,存栏量急剧下降,一时间猪肉价格暴涨,其他肉类价格也跟着大幅上扬,严重影响了居民的生活.为了解决这个问题,我国政府一方面鼓励有条件的企业和散户防控疫情,扩大生产;另一方面积极向多个国家开放猪肉进口,扩大肉源,确保市场供给稳定.某大型生猪生产企业分析当前市场形势,决定响应政府号召,扩大生产决策层调阅了该企业过去生产相关数据,就“一天中一头猪的平均成本与生猪存栏数量之间的关系”进行研究.现相关数据统计如下表:
生猪存栏数量 | 2 | 3 | 4 | 5 | 8 |
头猪每天平均成本 | 3.2 | 2.4 | 2 | 1.9 | 1.5 |
(1)研究员甲根据以上数据认为![]() 与
与![]() 具有线性回归关系,请帮他求出
具有线性回归关系,请帮他求出![]() 关于
关于![]() 的线.性回归方程
的线.性回归方程![]() (保留小数点后两位有效数字)
(保留小数点后两位有效数字)
(2)研究员乙根据以上数据得出![]() 与
与![]() 的回归模型:
的回归模型:![]() .为了评价两种模型的拟合效果,请完成以下任务:
.为了评价两种模型的拟合效果,请完成以下任务:
①完成下表(计算结果精确到0.01元)(备注:![]() 称为相应于点
称为相应于点![]() 的残差);
的残差);
生猪存栏数量 | 2 | 3 | 4 | 5 | 8 | |
头猪每天平均成本 | 3.2 | 2.4 | 2 | 1.9 | 1.5 | |
模型甲 | 估计值 | |||||
残差 | ||||||
模型乙 | 估计值 | 3.2 | 2.4 | 2 | 1.76 | 1.4 |
残差 | 0 | 0 | 0 | 0.14 | 0.1 | |
②分别计算模型甲与模型乙的残差平方和![]() 及
及![]() ,并通过比较
,并通过比较![]() 的大小,判断哪个模型拟合效果更好.
的大小,判断哪个模型拟合效果更好.
(3)根据市场调查,生猪存栏数量达到1万头时,饲养一头猪每一天的平均收入为7.5元;生猪存栏数量达到1.2万头时,饲养一头猪每一天的平均收入为7.2元若按(2)中拟合效果较好的模型计算一天中一头猪的平均成本,问该生猪存栏数量选择1万头还是1.2万头能获得更多利润?请说明理由.(利润=收入-成本)
参考公式: .
.
参考数据:![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com