
科目: 来源: 题型:
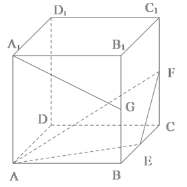
【题目】正方体![]() 的棱长为2,E,F,G分别为
的棱长为2,E,F,G分别为![]() ,
,![]() ,
,![]() 的中点,则( )
的中点,则( )
A.直线![]() 与直线
与直线![]() 垂直
垂直
B.直线![]() 与平面
与平面![]() 不平行
不平行
C.平面![]() 截正方体所得的截面面积为
截正方体所得的截面面积为![]()
D.点C与点G到平面![]() 的距离相等
的距离相等
查看答案和解析>>
科目: 来源: 题型:
【题目】在古装电视剧《知否》中,甲乙两人进行一种投壶比赛,比赛投中得分情况分“有初”“贯耳”“散射”“双耳”“依竿”五种,其中“有初”算“两筹”,“贯耳”算“四筹”,“散射”算“五筹”,“双耳”算“六筹”,“依竿”算“十筹”,三场比赛得筹数最多者获胜.假设甲投中“有初”的概率为![]() ,投中“贯耳”的概率为
,投中“贯耳”的概率为![]() ,投中“散射”的概率为
,投中“散射”的概率为![]() ,投中“双耳”的概率为
,投中“双耳”的概率为![]() ,投中“依竿”的概率为
,投中“依竿”的概率为![]() ,乙的投掷水平与甲相同,且甲乙投掷相互独立.比赛第一场,两人平局;第二场,甲投了个“贯耳”,乙投了个“双耳”,则三场比赛结束时,甲获胜的概率为( )
,乙的投掷水平与甲相同,且甲乙投掷相互独立.比赛第一场,两人平局;第二场,甲投了个“贯耳”,乙投了个“双耳”,则三场比赛结束时,甲获胜的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】某客户考察了一款热销的净水器,使用寿命为十年,改款净水器为三级过滤,每一级过滤都由核心部件滤芯来实现.在使用过程中,一级滤芯需要不定期更换,其中每更换![]() 个一级滤芯就需要更换
个一级滤芯就需要更换![]() 个二级滤芯,三级滤芯无需更换.其中一级滤芯每个
个二级滤芯,三级滤芯无需更换.其中一级滤芯每个![]() 元,二级滤芯每个
元,二级滤芯每个![]() 元.记一台净水器在使用期内需要更换的二级滤芯的个数构成的集合为
元.记一台净水器在使用期内需要更换的二级滤芯的个数构成的集合为![]() .如图是根据
.如图是根据![]() 台该款净水器在十年使用期内更换的一级滤芯的个数制成的柱状图.
台该款净水器在十年使用期内更换的一级滤芯的个数制成的柱状图.
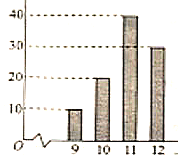
(1)结合图,写出集合![]() ;
;
(2)根据以上信息,求出一台净水器在使用期内更换二级滤芯的费用大于![]() 元的概率(以
元的概率(以![]() 台净水器更换二级滤芯的频率代替
台净水器更换二级滤芯的频率代替![]() 台净水器更换二级滤芯发生的概率);
台净水器更换二级滤芯发生的概率);
(3)若在购买净水器的同时购买滤芯,则滤芯可享受![]() 折优惠(使用过程中如需再购买无优惠).假设上述
折优惠(使用过程中如需再购买无优惠).假设上述![]() 台净水器在购机的同时,每台均购买
台净水器在购机的同时,每台均购买![]() 个一级滤芯、
个一级滤芯、![]() 个二级滤芯作为备用滤芯(其中
个二级滤芯作为备用滤芯(其中![]() ,
,![]() ),计算这
),计算这![]() 台净水器在使用期内购买滤芯所需总费用的平均数.并以此作为决策依据,如果客户购买净水器的同时购买备用滤芯的总数也为
台净水器在使用期内购买滤芯所需总费用的平均数.并以此作为决策依据,如果客户购买净水器的同时购买备用滤芯的总数也为![]() 个,则其中一级滤芯和二级滤芯的个数应分别是多少?
个,则其中一级滤芯和二级滤芯的个数应分别是多少?
查看答案和解析>>
科目: 来源: 题型:
【题目】已知抛物线![]() 与椭圆
与椭圆![]() 有一个相同的焦点,过点
有一个相同的焦点,过点![]() 且与
且与![]() 轴不垂直的直线
轴不垂直的直线![]() 与抛物线
与抛物线![]() 交于
交于![]() ,
,![]() 两点,
两点,![]() 关于
关于![]() 轴的对称点为
轴的对称点为![]() .
.
(1)求抛物线![]() 的方程;
的方程;
(2)试问直线![]() 是否过定点?若是,求出该定点的坐标;若不是,请说明理由.
是否过定点?若是,求出该定点的坐标;若不是,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
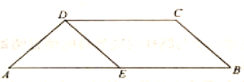
【题目】如图所示,在等腰梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 为
为![]() 的中点.将
的中点.将![]() 沿
沿![]() 折起,使点
折起,使点![]() 到达
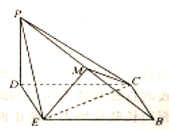
到达![]() 的位置,得到如图所示的四棱锥
的位置,得到如图所示的四棱锥![]() ,点
,点![]() 为棱
为棱![]() 的中点.
的中点.
(1)求证:![]() 平面
平面![]() ;
;
(2)若平面![]() 平面
平面![]() ,求三棱锥
,求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目: 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系,直线
轴正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的普通方程和直线
的普通方程和直线![]() 的直角坐标方程;
的直角坐标方程;
(2)射线![]() 的极坐标方程为
的极坐标方程为![]() ,若射线
,若射线![]() 与曲线
与曲线![]() 的交点为
的交点为![]() ,与直线
,与直线![]() 的交点为
的交点为![]() ,求线段
,求线段![]() 的长.
的长.
查看答案和解析>>
科目: 来源: 题型:
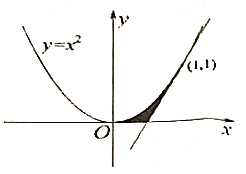
【题目】我国南北朝时期的数学家祖暅提出了计算体积的祖暅原理:“幂势既同,则积不容异。”意思是:两个等高的几何体若在所有等高处的水平截面的面积相等,则这两个几何体的体积相等.已知曲线![]() ,直线
,直线![]() 为曲线
为曲线![]() 在点
在点![]() 处的切线.如图所示,阴影部分为曲线
处的切线.如图所示,阴影部分为曲线![]() 、直线
、直线![]() 以及
以及![]() 轴所围成的平面图形,记该平面图形绕
轴所围成的平面图形,记该平面图形绕![]() 轴旋转一周所得的几何体为
轴旋转一周所得的几何体为![]() .给出以下四个几何体:
.给出以下四个几何体:


① ② ③ ④
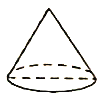
图①是底面直径和高均为![]() 的圆锥;
的圆锥;
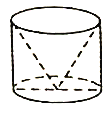
图②是将底面直径和高均为![]() 的圆柱挖掉一个与圆柱同底等高的倒置圆锥得到的几何体;
的圆柱挖掉一个与圆柱同底等高的倒置圆锥得到的几何体;
图③是底面边长和高均为![]() 的正四棱锥;
的正四棱锥;
图④是将上底面直径为![]() ,下底面直径为
,下底面直径为![]() ,高为
,高为![]() 的圆台挖掉一个底面直径为
的圆台挖掉一个底面直径为![]() ,高为
,高为![]() 的倒置圆锥得到的几何体.
的倒置圆锥得到的几何体.
根据祖暅原理,以上四个几何体中与![]() 的体积相等的是( )
的体积相等的是( )
A. ①B. ②C. ③D. ④
查看答案和解析>>
科目: 来源: 题型:
【题目】2019年1月1日,济南轨道交通![]() 号线试运行,济南轨道交通集团面向广大市民开展“参观体验,征求意见”活动,市民可以通过济南地铁APP抢票,小陈抢到了三张体验票,准备从四位朋友小王,小张,小刘,小李中随机选择两位与自己一起去参加体验活动,则小王被选中的概率为( )
号线试运行,济南轨道交通集团面向广大市民开展“参观体验,征求意见”活动,市民可以通过济南地铁APP抢票,小陈抢到了三张体验票,准备从四位朋友小王,小张,小刘,小李中随机选择两位与自己一起去参加体验活动,则小王被选中的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com