
科目: 来源: 题型:
【题目】设椭圆![]() ,直线
,直线![]() 经过点
经过点![]() ,直线
,直线![]() 经过点
经过点![]() ,直线
,直线![]() 直线
直线![]() ,且直线
,且直线![]() 分别与椭圆
分别与椭圆![]() 相交于
相交于![]() 两点和
两点和![]() 两点.
两点.
(Ⅰ)若![]() 分别为椭圆
分别为椭圆![]() 的左、右焦点,且直线
的左、右焦点,且直线![]() 轴,求四边形
轴,求四边形![]() 的面积;
的面积;
(Ⅱ)若直线![]() 的斜率存在且不为0,四边形
的斜率存在且不为0,四边形![]() 为平行四边形,求证:
为平行四边形,求证:![]() ;
;
(Ⅲ)在(Ⅱ)的条件下,判断四边形![]() 能否为矩形,说明理由.
能否为矩形,说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】2019年底,北京2022年冬奥组委会启动志愿者全球招募,仅一个月内报名人数便突破60万,其中青年学生约有50万人.现从这50万青年学生志愿者中,按男女分层抽样随机选取20人进行英语水平测试,所得成绩(单位:分)统计结果用茎叶图记录如下:
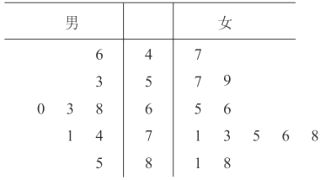
(Ⅰ)试估计在这50万青年学生志愿者中,英语测试成绩在80分以上的女生人数;
(Ⅱ)从选出的8名男生中随机抽取2人,记其中测试成绩在70分以上的人数为X,求![]() 的分布列和数学期望;
的分布列和数学期望;
(Ⅲ)为便于联络,现将所有的青年学生志愿者随机分成若干组(每组人数不少于5000),并在每组中随机选取![]() 个人作为联络员,要求每组的联络员中至少有1人的英语测试成绩在70分以上的概率大于90%.根据图表中数据,以频率作为概率,给出
个人作为联络员,要求每组的联络员中至少有1人的英语测试成绩在70分以上的概率大于90%.根据图表中数据,以频率作为概率,给出![]() 的最小值.(结论不要求证明)
的最小值.(结论不要求证明)
查看答案和解析>>
科目: 来源: 题型:
【题目】在四棱锥![]() 的底面
的底面![]() 中,
中,![]() ,
,![]() ,
,![]() 平面
平面![]() ,
,![]() 是
是![]() 的中点,且
的中点,且![]()

(Ⅰ)求证:![]() 平面
平面![]() ;
;
(Ⅱ)求二面角![]() 的余弦值;
的余弦值;
(Ⅲ)线段![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() ,若存在指出点
,若存在指出点![]() 的位置,若不存在请说明理由.
的位置,若不存在请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】在党中央的正确指导下,通过全国人民的齐心协力,特别是全体一线医护人员的奋力救治,二月份“新冠肺炎”疫情得到了控制.下图是国家卫健委给出的全国疫情通报,甲、乙两个省份从2月7日到2月13日一周的新增“新冠肺炎”确诊人数的折线图如下:

根据图中甲、乙两省的数字特征进行比对,通过比较把你得到最重要的两个结论写在答案纸指定的空白处.
①_________________________________________________.
②_________________________________________________.
查看答案和解析>>
科目: 来源: 题型:
【题目】2019年10月1日,庆祝中华人民共和国成立70周年大会、阅兵式、群众游行在北京隆重举行,这次阅兵编59个方(梯)队和联合军乐团,总规模约1.5万人,各型飞机160余架、装备580余套,是近几次阅兵中规模最大的一次.某机构统计了观看此次阅兵的年龄在30岁至80岁之间的100个观众,按年龄分组:第1组![]() ,第2组
,第2组![]() ,第3组
,第3组![]() ,第4组
,第4组![]() ,第5组
,第5组![]() ,得到的频率分布直方图如图所示.
,得到的频率分布直方图如图所示.

(1)求![]() 的值及这100个人的平均年龄(同一组中的数据用该组区间的中点值为代表);
的值及这100个人的平均年龄(同一组中的数据用该组区间的中点值为代表);
(2)用分层抽样的方法在年龄为![]() 、
、![]() 的人中抽取5人,再从抽取的5人中随机抽取2人接受采访,求接受采访的2人中年龄在
的人中抽取5人,再从抽取的5人中随机抽取2人接受采访,求接受采访的2人中年龄在![]() 的恰有1人的概率.
的恰有1人的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】科赫曲线是一种外形像雪花的几何曲线,一段科赫曲线可以通过下列操作步骤构造得到,任画一条线段,然后把它均分成三等分,以中间一段为边向外作正三角形,并把中间一段去掉,这样,原来的一条线段就变成了4条小线段构成的折线,称为“一次构造”;用同样的方法把每条小线段重复上述步骤,得到16条更小的线段构成的折线,称为“二次构造”,…,如此进行“![]() 次构造”,就可以得到一条科赫曲线.若要在构造过程中使得到的折线的长度达到初始线段的1000倍,则至少需要通过构造的次数是( ).(取
次构造”,就可以得到一条科赫曲线.若要在构造过程中使得到的折线的长度达到初始线段的1000倍,则至少需要通过构造的次数是( ).(取![]() ,
,![]() )
)
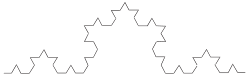
A.16B.17C.24D.25
查看答案和解析>>
科目: 来源: 题型:
【题目】下图统计了截止到2019年年底中国电动汽车充电桩细分产品占比及保有量情况,关于这5次统计,下列说法正确的是( )
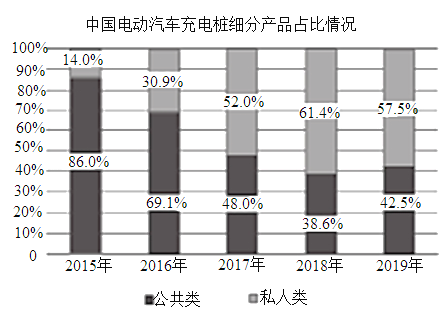
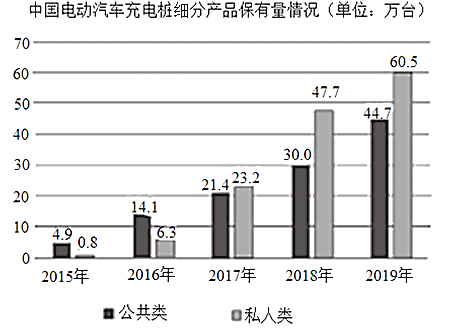
A.私人类电动汽车充电桩保有量增长率最高的年份是2018年
B.公共类电动汽车充电桩保有量的中位数是25.7万台
C.公共类电动汽车充电桩保有量的平均数为23.12万台
D.从2017年开始,我国私人类电动汽车充电桩占比均超过50%
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com