
科目: 来源: 题型:
【题目】体温是人体健康状况的直接反应,一般认为成年人腋下温度![]() (单位:
(单位:![]() )平均在
)平均在![]() 之间即为正常体温,超过
之间即为正常体温,超过![]() 即为发热.发热状态下,不同体温可分成以下三种发热类型:低热:
即为发热.发热状态下,不同体温可分成以下三种发热类型:低热:![]() ;高热:
;高热:![]() ;超高热(有生命危险):
;超高热(有生命危险):![]() .
.
某位患者因患肺炎发热,于12日至26日住院治疗. 医生根据病情变化,从14日开始,以3天为一个疗程,分别用三种不同的抗生素为该患者进行消炎退热. 住院期间,患者每天上午8:00服药,护士每天下午16:00为患者测量腋下体温记录如下:

(1)请你计算住院期间该患者体温不低于![]() 的各天体温平均值;
的各天体温平均值;
(2)在![]() 日—
日—![]() 日期间,医生会随机选取
日期间,医生会随机选取![]() 天在测量体温的同时为该患者进行某一特殊项目“
天在测量体温的同时为该患者进行某一特殊项目“![]() 项目”的检查,记
项目”的检查,记![]() 为高热体温下做“
为高热体温下做“![]() 项目”检查的天数,试求
项目”检查的天数,试求![]() 的分布列与数学期望;
的分布列与数学期望;
(3)抗生素治疗一般在服药后2-8个小时就能出现血液浓度的高峰,开始杀灭细菌,达到消炎退热效果.假设三种抗生素治疗效果相互独立,请依据表中数据,判断哪种抗生素治疗效果最佳,并说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】关于曲线![]() ,给出下列三个结论:
,给出下列三个结论:
① 曲线![]() 关于原点对称,但不关于
关于原点对称,但不关于![]() 轴、
轴、![]() 轴对称;
轴对称;
② 曲线![]() 恰好经过4个整点(即横、纵坐标均为整数的点);
恰好经过4个整点(即横、纵坐标均为整数的点);
③ 曲线![]() 上任意一点到原点的距离都不大于
上任意一点到原点的距离都不大于![]() .
.
其中,正确结论的序号是________.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知:①函数![]() ;
;
②向量![]() ,
,![]() ,且
,且![]() ,
,![]() ;
;
③函数![]() 的图象经过点
的图象经过点![]()
请在上述三个条件中任选一个,补充在下面问题中,并解答.
已知_________________,且函数![]() 的图象相邻两条对称轴之间的距离为
的图象相邻两条对称轴之间的距离为![]() .
.
(1)若![]() ,且
,且![]() ,求
,求![]() 的值;
的值;
(2)求函数![]() 在
在![]() 上的单调递减区间.
上的单调递减区间.
注:如果选择多个条件分别解答,按第一个解答计分.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数![]() .
.
(1)若曲线![]() 在
在![]() 处的切线与
处的切线与![]() 轴平行,求
轴平行,求![]() ;
;
(2)已知![]() 在
在![]() 上的最大值不小于
上的最大值不小于![]() ,求
,求![]() 的取值范围;
的取值范围;
(3)写出![]() 所有可能的零点个数及相应的
所有可能的零点个数及相应的![]() 的取值范围.(请直接写出结论)
的取值范围.(请直接写出结论)
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,过椭圆右焦点
,过椭圆右焦点![]() 的直线
的直线![]() 与椭圆交于
与椭圆交于![]() ,
,![]() 两点,当直线
两点,当直线![]() 与
与![]() 轴垂直时,
轴垂直时,![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)当直线![]() 与
与![]() 轴不垂直时,在
轴不垂直时,在![]() 轴上是否存在一点
轴上是否存在一点![]() (异于点
(异于点![]() ),使
),使![]() 轴上任意点到直线
轴上任意点到直线![]() ,
,![]() 的距离均相等?若存在,求
的距离均相等?若存在,求![]() 点坐标;若不存在,请说明理由.
点坐标;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】关于函数![]() ,有以下三个结论:
,有以下三个结论:
①函数恒有两个零点,且两个零点之积为![]() ;
;
②函数的极值点不可能是![]() ;
;
③函数必有最小值.
其中正确结论的个数有( )
A.0个B.1个C.2个D.3个
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为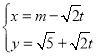 (其中
(其中![]() 为参数,
为参数,![]() ).以坐标原点
).以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,
,![]() 被
被![]() 截得的弦长为
截得的弦长为![]() .
.
(1)求实数![]() 的值;
的值;
(2)设![]() 与
与![]() 交于点
交于点![]() ,
,![]() ,若点
,若点![]() 的坐标为
的坐标为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】2014年,中央和国务院办公厅印发《关于引导农村土地经营权有序流转发展农业适度规模经营的意见》,要求大力发展土地流转和适度规模经营.某种粮大户2015年开始承包了一地区的大规模水田种植水稻,购买了一种水稻收割机若干台,这种水稻收割机随着使用年限的增加,每年的养护费也相应增加,这批水稻收割机自购买使用之日起,5年以来平均每台水稻收割机的养护费用数据统计如下:
年份 | 2015 | 2016 | 2017 | 2018 | 2019 |
年份代码 | 1 | 2 | 3 | 4 | 5 |
养护费用 | 1.1 | 1.6 | 2 | 2.5 | 2.8 |
(1)从这5年中随机抽取2年,求平均每台水稻收割机每年的养护费用至少有1年多于2万元的概率;
(2)求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(3)若该水稻收割机的购买价格是每台16万元,由(2)中的回归方程,从每台水稻收割机的年平均费用角度,你认为一台该水稻收割机是使用满5年就淘汰,还是继续使用到满8年再淘汰?
附:回归直线的斜率和截距的最小二乘法估计公式分别为: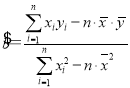 ,
,![]()
![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】对于正整数![]() ,如果
,如果![]() 个整数
个整数![]() 满足
满足![]() ,
,
且![]() ,则称数组
,则称数组![]() 为
为![]() 的一个“正整数分拆”.记
的一个“正整数分拆”.记![]() 均为偶数的“正整数分拆”的个数为
均为偶数的“正整数分拆”的个数为![]() 均为奇数的“正整数分拆”的个数为
均为奇数的“正整数分拆”的个数为![]() .
.
(Ⅰ)写出整数4的所有“正整数分拆”;
(Ⅱ)对于给定的整数![]() ,设
,设![]() 是
是![]() 的一个“正整数分拆”,且
的一个“正整数分拆”,且![]() ,求
,求![]() 的最大值;
的最大值;
(Ⅲ)对所有的正整数![]() ,证明:
,证明:![]() ;并求出使得等号成立的
;并求出使得等号成立的![]() 的值.
的值.
(注:对于![]() 的两个“正整数分拆”
的两个“正整数分拆”![]() 与
与![]() ,当且仅当
,当且仅当![]() 且
且![]() 时,称这两个“正整数分拆”是相同的.)
时,称这两个“正整数分拆”是相同的.)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com