
科目: 来源: 题型:
【题目】已知抛物线C:x24py(p为大于2的质数)的焦点为F,过点F且斜率为k(k0)的直线交C于A,B两点,线段AB的垂直平分线交y轴于点E,抛物线C在点A,B处的切线相交于点G.记四边形AEBG的面积为S.
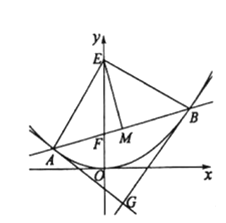
(1)求点G的轨迹方程;
(2)当点G的横坐标为整数时,S是否为整数?若是,请求出所有满足条件的S的值;若不是,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】某商店举行促销反馈活动,顾客购物每满200元,有一次抽奖机会(即满200元可以抽奖一次,满400元可以抽奖两次,依次类推).抽奖的规则如下:在一个不透明口袋中装有编号分别为1,2,3,4,5的5个完全相同的小球,顾客每次从口袋中摸出一个小球,共摸三次,每次摸出的小球均不放回口袋,若摸得的小球编号一次比一次大(如1,2,5),则获得一等奖,奖金40元;若摸得的小球编号一次比一次小(如5,3,1),则获得二等奖,奖金20元;其余情况获得三等奖,奖金10元.
(1)某人抽奖一次,求其获奖金额X的概率分布和数学期望;
(2)赵四购物恰好满600元,假设他不放弃每次抽奖机会,求他获得的奖金恰好为60元的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知数列![]() ,
,![]() ,数列
,数列![]() 满足
满足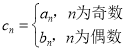 ,n
,n![]() .
.
(1)若![]() ,
,![]() ,求数列
,求数列![]() 的前2n项和
的前2n项和![]() ;
;
(2)若数列![]() 为等差数列,且对任意n
为等差数列,且对任意n![]() ,
,![]() 恒成立.
恒成立.
①当数列![]() 为等差数列时,求证:数列
为等差数列时,求证:数列![]() ,
,![]() 的公差相等;
的公差相等;
②数列![]() 能否为等比数列?若能,请写出所有满足条件的数列
能否为等比数列?若能,请写出所有满足条件的数列![]() ;若不能,请说明理由.
;若不能,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数![]() (m
(m![]() R)的导函数为
R)的导函数为![]() .
.
(1)若函数![]() 存在极值,求m的取值范围;
存在极值,求m的取值范围;
(2)设函数![]() (其中e为自然对数的底数),对任意m
(其中e为自然对数的底数),对任意m![]() R,若关于x的不等式
R,若关于x的不等式![]() 在(0,
在(0,![]() )上恒成立,求正整数k的取值集合.
)上恒成立,求正整数k的取值集合.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,已知椭圆C:![]() (a>b>0)的离心率为
(a>b>0)的离心率为![]() .且经过点(1,
.且经过点(1,![]() ),A,B分别为椭圆C的左、右顶点,过左焦点F的直线l交椭圆C于D,E两点(其中D在x轴上方).
),A,B分别为椭圆C的左、右顶点,过左焦点F的直线l交椭圆C于D,E两点(其中D在x轴上方).

(1)求椭圆C的标准方程;
(2)若△AEF与△BDF的面积之比为1:7,求直线l的方程.
查看答案和解析>>
科目: 来源: 题型:
【题目】某地为改善旅游环境进行景点改造.如图,将两条平行观光道l1和l2通过一段抛物线形状的栈道AB连通(道路不计宽度),l1和l2所在直线的距离为0.5(百米),对岸堤岸线l3平行于观光道且与l2相距1.5(百米)(其中A为抛物线的顶点,抛物线的对称轴垂直于l3,且交l3于M),在堤岸线l3上的E,F两处建造建筑物,其中E,F到M的距离为1(百米),且F恰在B的正对岸(即BF⊥l3).
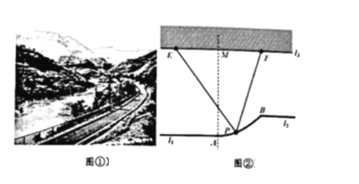
(1)在图②中建立适当的平面直角坐标系,并求栈道AB的方程;
(2)游客(视为点P)在栈道AB的何处时,观测EF的视角(∠EPF)最大?请在(1)的坐标系中,写出观测点P的坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在四棱锥P—ABCD中,四边形ABCD为平行四边形,BD⊥DC,△PCD为正三角形,平面PCD⊥平面ABCD,E为PC的中点.
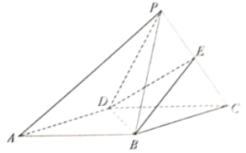
(1)证明:AP∥平面EBD;
(2)证明:BE⊥PC.
查看答案和解析>>
科目: 来源: 题型:
【题目】假如你的公司计划购买台机器,该种机器使用三年后即被淘汰,在购进机器时,可以一次性额外购买几次维修服务,每次维修服务费用200元,另外实际维修一次还需向维修人员支付小费,小费每次50元,在机器使用期间,如果维修次数超过购机时购买的维修服务次数,则每维修一次需支付维修服务费用500元,无需支付小费,现需决策在购买机器时应同时一次性购买几次维修服务,为此搜集并整理了100台这种机器在三年使用期内的维修次数,得下面统计表:
维修次数 | 8 | 9 | 10 | 11 | 12 |
频数 | 10 | 20 | 30 | 30 | 10 |
记![]() 表示1台机器在三年使用期内的维修次数,
表示1台机器在三年使用期内的维修次数,![]() 表示1台机器在维修上所需的费用(单位:元),
表示1台机器在维修上所需的费用(单位:元),![]() 表示购机的同时购买的维修服务次数.
表示购机的同时购买的维修服务次数.
(1)若![]() ,求
,求![]() 与
与![]() 的函数解析式.
的函数解析式.
(2)若要求“维修次数不大于![]() ”的频率不小于0.8,求
”的频率不小于0.8,求![]() 的值.
的值.
(3)假设这100台机器在购机的同时每台都购买10次维修服务,或每台都购买11次维修服务,分别计算这100台机器在维修上所需费用的平均数,以此作为决策依据,购买1台机器的同时应购买10次还是11次维修服务?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com