
科目: 来源: 题型:
【题目】为抗击新型冠状病毒,普及防护知识,某校开展了“疫情防护”网络知识竞赛活动.现从参加该活动的学生中随机抽取了100名学生,将他们的比赛成绩(满分为100分)分为6组:![]() ,得到如图所示的频率分布直方图.
,得到如图所示的频率分布直方图.
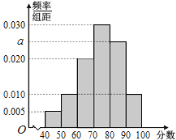
(1)求![]() 的值,并估计这100名学生的平均成绩(同一组中的数据用该组区间的中点值为代表);
的值,并估计这100名学生的平均成绩(同一组中的数据用该组区间的中点值为代表);
(2)在抽取的100名学生中,规定:比赛成绩不低于80分为“优秀”,比赛成绩低于80分为“非优秀”.请将下面的2×2列联表补充完整,并判断是否有99%的把握认为“比赛成绩是否优秀与性别有关”?
优秀 | 非优秀 | 合计 | |
男生 | 40 | ||
女生 | 50 | ||
合计 | 100 |
参考公式及数据:![]() .
.
| 0.05 | 0.01 | 0.005 | 0.001 |
| 3.841 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目: 来源: 题型:
【题目】已知直线![]() 的参数方程为
的参数方程为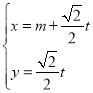 (
(![]() 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,且曲线
,且曲线![]() 的左焦点
的左焦点![]() 在直线
在直线![]() 上.
上.
(Ⅰ)求![]() 的极坐标方程和曲线
的极坐标方程和曲线![]() 的参数方程;
的参数方程;
(Ⅱ)求曲线![]() 的内接矩形的周长的最大值.
的内接矩形的周长的最大值.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知![]() ,如图,曲线
,如图,曲线![]() 由曲线
由曲线![]() :
:![]() 和曲线
和曲线![]() :
:![]() 组成,其中点
组成,其中点![]() 为曲线
为曲线![]() 所在圆锥曲线的焦点,点
所在圆锥曲线的焦点,点![]() 为曲线
为曲线![]() 所在圆锥曲线的焦点.
所在圆锥曲线的焦点.
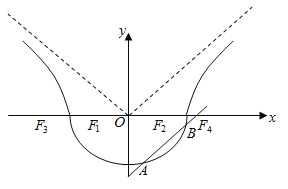
(Ⅰ)若![]() ,求曲线
,求曲线![]() 的方程;
的方程;
(Ⅱ)如图,作直线![]() 平行于曲线
平行于曲线![]() 的渐近线,交曲线
的渐近线,交曲线![]() 于点
于点![]() ,求证:弦
,求证:弦![]() 的中点
的中点![]() 必在曲线
必在曲线![]() 的另一条渐近线上;
的另一条渐近线上;
(Ⅲ)对于(Ⅰ)中的曲线![]() ,若直线
,若直线![]() 过点
过点![]() 交曲线
交曲线![]() 于点
于点![]() ,求
,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数![]() ,
,![]()
![]() .
.
(1)当x≥0时,f(x)≤h(x)恒成立,求a的取值范围;
(2)当x<0时,研究函数F(x)=h(x)﹣g(x)的零点个数;
(3)求证:![]() (参考数据:ln1.1≈0.0953).
(参考数据:ln1.1≈0.0953).
查看答案和解析>>
科目: 来源: 题型:
【题目】班主任为了对本班学生的考试成绩进行分析,决定从本班24名女同学,18名男同学中随机抽取一个容量为7的样本进行分析.
(1)如果按照性别比例分层抽样,可以得到多少个不同的样本?(写出算式即可,不必计算出结果)
(2)如果随机抽取的7名同学的数学,物理成绩(单位:分)对应如下表:
学生序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
数学成绩 | 60 | 65 | 70 | 75 | 85 | 87 | 90 |
物理成绩 | 70 | 77 | 80 | 85 | 90 | 86 | 93 |
①若规定85分以上(包括85分)为优秀,从这7名同学中抽取3名同学,记3名同学中数学和物理成绩均为优秀的人数为![]() ,求
,求![]() 的分布列和数学期望;
的分布列和数学期望;
②根据上表数据,求物理成绩![]() 关于数学成绩
关于数学成绩![]() 的线性回归方程(系数精确到0.01);若班上某位同学的数学成绩为96分,预测该同学的物理成绩为多少分?
的线性回归方程(系数精确到0.01);若班上某位同学的数学成绩为96分,预测该同学的物理成绩为多少分?
附:线性回归方程![]() ,
,
其中 ,
,![]() .
.
|
|
|
|
76 | 83 | 812 | 526 |
查看答案和解析>>
科目: 来源: 题型:
【题目】下列判断错误的是( )
A.若随机变量![]() 服从正态分布
服从正态分布![]() ,则
,则![]()
B.已知直线![]()
![]() 平面
平面![]() ,直线
,直线![]() 平面
平面![]() ,则“
,则“![]() ”是“
”是“![]() ”的充分不必要条件
”的充分不必要条件
C.若随机变量![]() 服从二项分布:
服从二项分布: ![]() , 则
, 则![]()
D.![]() 是
是![]() 的充分不必要条件
的充分不必要条件
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆![]() ,焦距为2,离心率
,焦距为2,离心率![]() 为
为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)过点![]() 作圆
作圆![]() 的切线,切点分别为
的切线,切点分别为![]() ,直线
,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,过点
,过点![]() 的直线
的直线![]() 交椭圆
交椭圆![]() 于
于![]() 两点,点
两点,点![]() 关于
关于![]() 轴的对称点为
轴的对称点为![]() ,求
,求![]() 的面积的最大值.
的面积的最大值.
查看答案和解析>>
科目: 来源: 题型:
【题目】二手车经销商小王对其所经营的A型号二手汽车的使用年数x与销售价格y(单位:万元/辆)进行整理,得到如下数据:
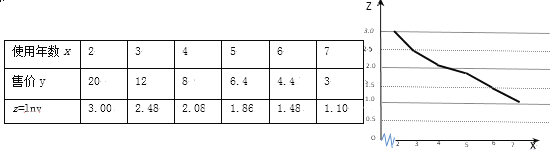
如图是z关于x的折线图:
(1)由折线图可以看出,可以用线性回归模型拟合z和x的关系,请用相关系数r加以说明(注:若相关系数︱r︱![]() 0.75,则认为两个变量相关程度较强);
0.75,则认为两个变量相关程度较强);
(2)求y关于x的回归方程并预测某辆A型号二手车当使用年数为9年时售价约为多少?(![]() 小数点后面保留两位有效数字);
小数点后面保留两位有效数字);
(3)基于成本的考虑,该型号二手车的售价不得低于7118元,请根据(2)求出的回归方程预测在收购该型号的二手车时车辆的使用年限不得超过多少年?
参考公式:回归方程![]() 中斜率和截距的最小二乘法估计公式分别为:
中斜率和截距的最小二乘法估计公式分别为:
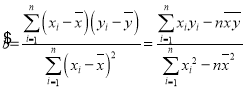 ,
,
参考数据: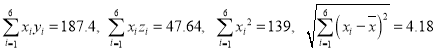
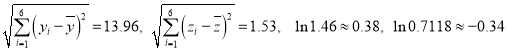
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com