
科目: 来源: 题型:
【题目】2019年全国“两会”,即中华人民共和国第十三届全国人大二次会议和中国人民政治协商会议第十三届全国委员会第二次会议,分别于2019年3月5日和3月3日在北京召开.为了了解哪些人更关注“两会”,某机构随机抽取了年龄在![]() 岁之间的200人进行调查.并按年龄绘制的频率分布直方图如图所示,把年龄落在区间
岁之间的200人进行调查.并按年龄绘制的频率分布直方图如图所示,把年龄落在区间![]() 和
和![]() 内的人分别称为“青少年人”和“中老年人”
内的人分别称为“青少年人”和“中老年人”![]() 经统计“青少年人”和“中老年人”的人数之比为
经统计“青少年人”和“中老年人”的人数之比为![]() ,其中“青少年人”中有40人关注“两会”,“中老年人”中关注“两会”和不关注“两会”的人数之比是
,其中“青少年人”中有40人关注“两会”,“中老年人”中关注“两会”和不关注“两会”的人数之比是![]() .
.
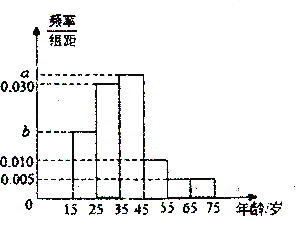
(1)求图中a,b的值;
(2)现采用分层抽样在![]() 和
和![]() 中随机抽取8名代表,从8人中任选2人,求2人中至少有1个是“中老年人”的概率是多少?
中随机抽取8名代表,从8人中任选2人,求2人中至少有1个是“中老年人”的概率是多少?
(3)根据已知条件,完成下面的![]() 列联表,并根据此统计结果判断:能否有
列联表,并根据此统计结果判断:能否有![]() 的把握认为“中老年人”比“青少年人”更加关注“两会”?
的把握认为“中老年人”比“青少年人”更加关注“两会”?
关注 | 不关注 | 合计 | |
青少年人 | |||
中老年人 | |||
合计 |
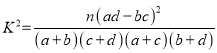
P(K2≥k0) | 0.50 | 0.40 | … | 0.010 | 0.005 | 0.001 |
k0 | 0.455 | 0.708 | … | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() ,过点
,过点![]() 的直线与椭圆
的直线与椭圆![]() 交于
交于![]() 两点,延长
两点,延长![]() 交椭圆
交椭圆![]() 于点
于点![]() ,
,![]() 的周长为8.
的周长为8.

(1)求![]() 的离心率及方程;
的离心率及方程;
(2)试问:是否存在定点![]() ,使得
,使得![]() 为定值?若存在,求
为定值?若存在,求![]() ;若不存在,请说明理由.
;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】奇函数f(x)在R上存在导数![]() ,当x<0时,
,当x<0时,![]()
![]() f(x),则使得(x2﹣1)f(x)<0成立的x的取值范围为( )
f(x),则使得(x2﹣1)f(x)<0成立的x的取值范围为( )
A.(﹣1,0)∪(0,1)B.(﹣∞,﹣1)∪(0,1)
C.(﹣1,0)∪(1,+∞)D.(﹣∞,﹣1)∪(1,+∞)
查看答案和解析>>
科目: 来源: 题型:
【题目】某工厂生产某种电子产品,每件产品不合格的概率均为![]() ,现工厂为提高产品声誉,要求在交付用户前每件产品都通过合格检验,已知该工厂的检验仪器一次最多可检验
,现工厂为提高产品声誉,要求在交付用户前每件产品都通过合格检验,已知该工厂的检验仪器一次最多可检验![]() 件该产品,且每 件产品检验合格与否相互独立.若每件产品均检验一次,所需检验费用较多,该工厂提出以下检 验方案:将产品每
件该产品,且每 件产品检验合格与否相互独立.若每件产品均检验一次,所需检验费用较多,该工厂提出以下检 验方案:将产品每![]() 个
个![]() 一组进行分组检验,如果某一组产品检验合格,则说明该组内产品均合格,若检验不合格,则说明该组内有不合格产品,再对该组内每一件产品单独进行检验,如此,每一组产品只需检验
一组进行分组检验,如果某一组产品检验合格,则说明该组内产品均合格,若检验不合格,则说明该组内有不合格产品,再对该组内每一件产品单独进行检验,如此,每一组产品只需检验![]() 次或
次或![]() 次.设该工厂生产
次.设该工厂生产![]() 件该产品,记每件产品的平均检验次 数为
件该产品,记每件产品的平均检验次 数为![]() .
.
(1)求![]() 的分布列及其期望;
的分布列及其期望;
(2)(i)试说明,当![]() 越小时,该方案越合理,即所需平均检验次数越少;
越小时,该方案越合理,即所需平均检验次数越少;
(ii)当![]() 时,求使该方案最合理时
时,求使该方案最合理时![]() 的值及
的值及![]() 件该产品的平均检验次数.
件该产品的平均检验次数.
查看答案和解析>>
科目: 来源: 题型:
【题目】为实现国民经济新“三步走”的发展战略目标,国家加大了扶贫攻坚的力度.某地区在2015 年以前的年均脱贫率(脱离贫困的户数占当年贫困户总数的比)为![]() .2015年开始,全面实施“精准扶贫”政策后,扶贫效果明显提高,其中2019年度实施的扶贫项目,各项目参加户数占比(参加该项目户数占 2019 年贫困户总数的比)及该项目的脱贫率见下表:
.2015年开始,全面实施“精准扶贫”政策后,扶贫效果明显提高,其中2019年度实施的扶贫项目,各项目参加户数占比(参加该项目户数占 2019 年贫困户总数的比)及该项目的脱贫率见下表:
实施项目 | 种植业 | 养殖业 | 工厂就业 | 服务业 |
参加用户比 |
|
|
|
|
脱贫率 |
|
|
|
|
那么![]() 年的年脱贫率是实施“精准扶贫”政策前的年均脱贫率的( )
年的年脱贫率是实施“精准扶贫”政策前的年均脱贫率的( )
A.![]() 倍B.
倍B.![]() 倍C.
倍C.![]() 倍D.
倍D.![]() 倍
倍
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆![]() (
(![]() )的离心率为
)的离心率为![]() ,以
,以![]() 的短轴为直径的圆与直线
的短轴为直径的圆与直线![]() 相切.
相切.
(1)求![]() 的方程;
的方程;
(2)直线![]() 交
交![]() 于
于![]() ,
,![]() 两点,且
两点,且![]() .已知
.已知![]() 上存在点
上存在点![]() ,使得
,使得![]() 是以
是以![]() 为顶角的等腰直角三角形,若
为顶角的等腰直角三角形,若![]() 在直线
在直线![]() 的右下方,求
的右下方,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com