
科目: 来源: 题型:
【题目】惠州市某商店销售某海鲜,经理统计了春节前后50天该海鲜的日需求量![]() (
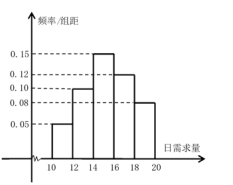
(![]() ,单位:公斤),其频率分布直方图如下图所示.该海鲜每天进货1次,每销售1公斤可获利40元;若供大于求,剩余的海鲜削价处理,削价处理的海鲜每公斤亏损10元;若供不应求,可从其它商店调拨,调拨的海鲜销售1公斤可获利30元.假设商店该海鲜每天的进货量为14公斤,商店销售该海鲜的日利润为
,单位:公斤),其频率分布直方图如下图所示.该海鲜每天进货1次,每销售1公斤可获利40元;若供大于求,剩余的海鲜削价处理,削价处理的海鲜每公斤亏损10元;若供不应求,可从其它商店调拨,调拨的海鲜销售1公斤可获利30元.假设商店该海鲜每天的进货量为14公斤,商店销售该海鲜的日利润为![]() 元.
元.
(1)求商店日利润![]() 关于日需求量
关于日需求量![]() 的函数表达式.
的函数表达式.
(2)根据频率分布直方图,
①估计这50天此商店该海鲜日需求量的平均数.
②假设用事件发生的频率估计概率,请估计日利润不少于620元的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知![]() 是椭圆
是椭圆![]() 的两个焦点,
的两个焦点,![]() 是椭圆
是椭圆![]() 上一点,当
上一点,当![]() 时,有
时,有![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设过椭圆右焦点![]() 的动直线
的动直线![]() 与椭圆交于
与椭圆交于![]() 两点,试问在
两点,试问在![]() 铀上是否存在与
铀上是否存在与![]() 不重合的定点
不重合的定点![]() ,使得
,使得![]() 恒成立?若存在,求出定点
恒成立?若存在,求出定点![]() 的坐标,若不存在,请说明理由.
的坐标,若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】在直角坐标系.xOy中,曲线C1的参数方程为![]() (
(![]() 为参数),以原点O为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρ=4sinθ.
为参数),以原点O为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρ=4sinθ.
(1)求曲线C1的普通方程和C2的直角坐标方程;
(2)已知曲线C2的极坐标方程为![]() ,点A是曲线C3与C1的交点,点B是曲线C3与C2的交点,且A,B均异于原点O,且|AB|=4
,点A是曲线C3与C1的交点,点B是曲线C3与C2的交点,且A,B均异于原点O,且|AB|=4![]() ,求α的值.
,求α的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】近年来,在新高考改革中,打破文理分科的“![]() ”模式初露端倪,其中语、数、外三门课为必考科目,剩下三门为选考科目选考科目成绩采用“赋分制”,即原始分数不直接用,而是按照学生分数在本科目考试的排名来划分等级并以此打分得到最后得分,假定
”模式初露端倪,其中语、数、外三门课为必考科目,剩下三门为选考科目选考科目成绩采用“赋分制”,即原始分数不直接用,而是按照学生分数在本科目考试的排名来划分等级并以此打分得到最后得分,假定![]() 省规定:选考科目按考生成绩从高到低排列,按照占总体
省规定:选考科目按考生成绩从高到低排列,按照占总体![]() 、
、![]() 、
、![]() 、
、![]() 分别赋分
分别赋分![]() 分、
分、![]() 分、
分、![]() 分、
分、![]() 分,为了让学生们体验“赋分制”计算成绩的方法,
分,为了让学生们体验“赋分制”计算成绩的方法,![]() 省某高中高一(
省某高中高一(![]() )班(共
)班(共![]() 人)举行了以此摸底考试(选考科目全考,单料全班排名),知这次摸底考试中的物理成绩(满分
人)举行了以此摸底考试(选考科目全考,单料全班排名),知这次摸底考试中的物理成绩(满分![]() 分)频率分布直方图,化学成绩(满分
分)频率分布直方图,化学成绩(满分![]() 分)茎叶图如图所示,小明同学在这次考试中物理
分)茎叶图如图所示,小明同学在这次考试中物理![]() 分,化学
分,化学![]() 多分.
多分.

(1)采用赋分制后,求小明物理成绩的最后得分;
(2)若小明的化学成绩最后得分为![]() 分,求小明的原始成绩的可能值;
分,求小明的原始成绩的可能值;
(3)若小明必选物理,其他两科从化学、生物、历史、地理、政治五科中任选,求小明此次考试选考科目包括化学的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】天气预报说,今后三天每天下雨的概率相同,现用随机模拟的方法预测三天中有两天下雨的概率,用骰子点数来产生随机数.依据每天下雨的概率,可规定投一次骰子出现1点和2点代表下雨;投三次骰子代表三天;产生的三个随机数作为一组.得到的10组随机数如下:613,265,114,236,561,435,443,251,154,353.则在此次随机模拟试验中,每天下雨的概率的近似值是__________,三天中有两天下雨的概率的近似值为__________
查看答案和解析>>
科目: 来源: 题型:
【题目】程大位是明代著名数学家,他的《新编直指算法统宗》是中国历史上一部影响巨大的著作.卷八中第33问:“今有三角果一垛,底阔每面七个.问该若干?”如图是解决该问题的程序框图.执行该程序框图,求得该垛果子的总数S为( )
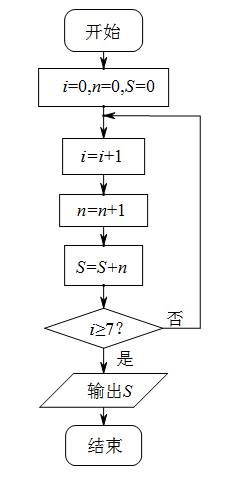
A.28B.56C.84D.120
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com