
科目: 来源: 题型:
【题目】将编号为1,2,3,4,5,6,7的小球放入编号为1,2,3,4,5,6,7的七个盒子中,每盒放一球,若有且只有三个盒子的编号与放入的小球的编号相同,则不同的放法种数为( ).
A.5040B.24C.315D.840
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),直线
为参数),直线![]() 与曲线
与曲线![]()
![]() 交于
交于![]() 两点.
两点.
(1)求![]() 的长;
的长;
(2)在以![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立的极坐标系中,设点
轴的正半轴为极轴建立的极坐标系中,设点![]() 的极坐标为
的极坐标为![]() ,求点
,求点![]() 到线段
到线段![]() 中点
中点![]() 的距离.
的距离.
查看答案和解析>>
科目: 来源: 题型:
【题目】传染病的流行必须具备的三个基本环节是:传染源、传播途径和人群易感性.三个环节必须同时存在,方能构成传染病流行.呼吸道飞沫和密切接触传播是新冠状病毒的主要传播途径,为了有效防控新冠状病毒的流行,人们出行都应该佩戴口罩.某地区已经出现了新冠状病毒的感染病人,为了掌握该地区居民的防控意识和防控情况,用分层抽样的方法从全体居民中抽出一个容量为100的样本,统计样本中每个人出行是否会佩戴口罩的情况,得到下面列联表:
戴口罩 | 不戴口罩 | |
青年人 | 50 | 10 |
中老年人 | 20 | 20 |
(1)能否有![]() 的把握认为是否会佩戴口罩出行的行为与年龄有关?
的把握认为是否会佩戴口罩出行的行为与年龄有关?
(2)用样本估计总体,若从该地区出行不戴口罩的居民中随机抽取5人,求恰好有2人是青年人的概率.
附: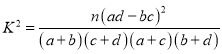
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目: 来源: 题型:
【题目】将函数![]() 向左平移
向左平移![]() 个单位,得到
个单位,得到![]() 的图象,则
的图象,则![]() 满足( )
满足( )
A.图象关于点![]() 对称,在区间
对称,在区间![]() 上为增函数
上为增函数
B.函数最大值为2,图象关于点![]() 对称
对称
C.图象关于直线![]() 对称,在
对称,在![]() 上的最小值为1
上的最小值为1
D.最小正周期为![]() ,
,![]() 在
在![]() 有两个根
有两个根
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com